Question
Question: In the given diagram pulley is massless and frictionless. Strings and spring are ideal. If the strin...
In the given diagram pulley is massless and frictionless. Strings and spring are ideal. If the string is taut during the motion of the block of mass ‘m’. Calculate the time period of small oscillation.
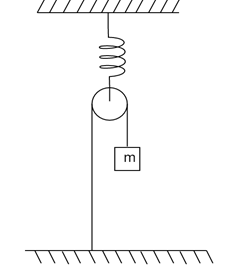
Solution
Hint To solve this type of problem, the first step is to find the mean position of the spring-mass system i.e. the normal length of the spring is the position of the equilibrium point. The second step is to displace the object from its mean position, the restoring force will act on the body. The third step is to calculate the acceleration of the body and then substitute the value in the formula of the time period.
Complete step-by-step answer
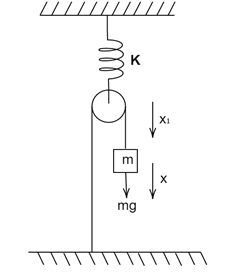
Let in equilibrium position of the block, elongation in spring is x0
F=kx0 .............(1)
Let Tension in the thread is T at the equilibrium position
kx0=2T ............. (2)
Also at the equilibrium position, the force balances the spring force is the gravitational force
Therefore, using the equation (1) and (2) we get,
mg=T=2kx0 ...............(3)
Displace the block by x from its equilibrium position in the downward direction, Let the pulley moves a distance x1 .So the length of thread available for the block to fall:
⇒x=2x1................. (4)
Let T1 be the tension acting on block in an upward direction after displacement,
2T1=k(x0+x1)
Using equation (3) and (4) we get,
⇒T1=2k(k2mg+2x) ..................(5)
Therefore, The net Force on the block in this position,
Fnet=(T1−mg)
On putting the value of T1 from equation (5)
⇒Fnet=2k(k2mg+2x)−mg
⇒mg+4kx−mg=(4k)×x ..................(6)
The net force on the block is
⇒Fnet=ma
On equating the above equations we get,
⇒ma=(4k)×x
⇒a=(4mk)×x
The relation between acceleration and angular velocity is given as
⇒ω2x=a
Substituting the value of a in the above relation, we get
⇒ω2x=(4mk)×x
⇒ω=4mk
The relation between ω and time period is given as
⇒T=ω2π
Substituting the value of ω in the above relation, we get
⇒T=2πk4m
Note As the block is left hanging it will experience a constant downward force by the earth. At the same time, it will also experience a force by the spring. Thus as a whole, it will start doing simple harmonic motion at some mean point with some amplitude.
