Question
Question: In the given circuit what is the maximum value of \( R_S \) for a zener diode to regulate voltage on...
In the given circuit what is the maximum value of RS for a zener diode to regulate voltage on load resistance?
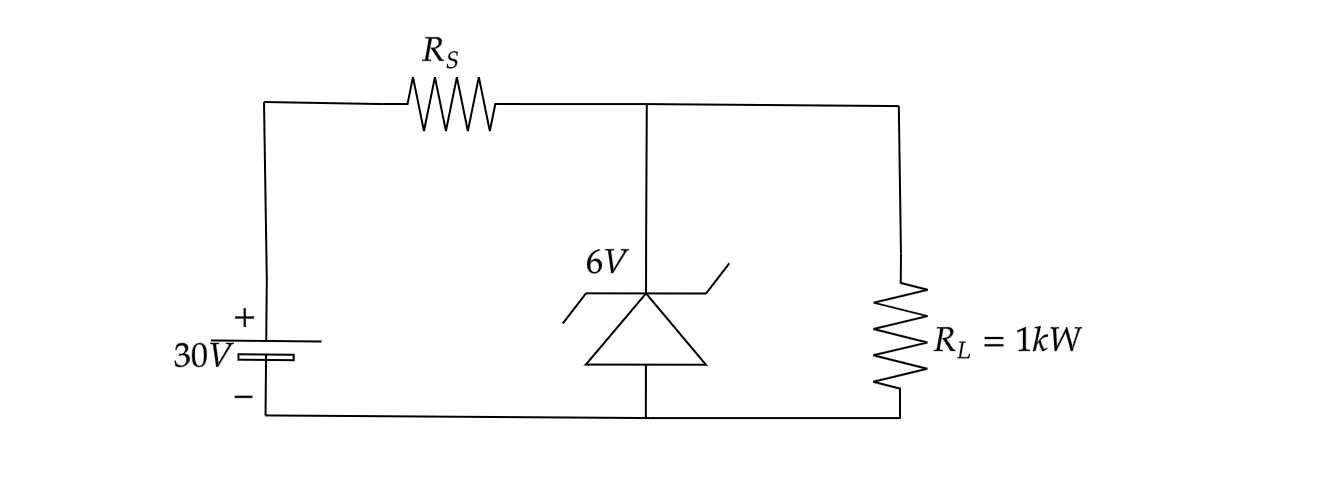
(A)2kΩ
(B)5kΩ
(C)6kΩ
(D)4kΩ
Solution
There is a mistake in the question that the value of load resistance is given in matt it should be in ohm. If calculated by taking its power then the solution will not match with the optio. Hence we will solve by taking load resistance on kiloohm. To satisfy the given condition the voltage across the load must be equal to the enor voltage. Then using ohm’s law in the further step we can calculate the value of RS .
Complete answer:
As per the problem we need to calculate the maximum value of RS for a zener diode to regulate voltage on load resistance.
Now the zener diode to regulate voltage on load resistance we can write it as,
VRL=VZ……(1)
Where,
The voltage across the load resistance is represent as VRL
And the voltage across zener diode is represented as VZ
Now in place of VRL we can write,
VRL=IRL……(2)
Now using ohm's law on current value we will get,
I=ReqV
Here the load resistance and RS are connected in series,
Hence the equivalent resistance be,
Req=RS+RL
Now putting the value in the above current equation we will get,
I=RS+RLV
Putting this value in the above equation (2) we will get,
VRL=RS+RLVRL……(3)
Putting equation (3) in place of equation (1) we will get,
RS+RLVRL=VZ
From the figure we know,
V=30V
RL=1kΩ
VZ=6V
Now putting these values we will get,
RS+1kΩ30V×1kΩ=6V
Cancelling the terms we will get,
RS+1kΩ5kΩ=1
Rearranging the above equation we will egt,
5kΩ=RS+1kΩ
Hence the value of RS=4kΩ .
Therefore the correct option is (D) .
Note:
Here the zener diode is also called voltage regulator only reverse biased because it is specially made to have a reverse voltage breakdown at a specific voltage. Note that if the zener diode is biased in the forward direction it behaves like a normal signal passing the current increasing linearly with voltage, now in this case it will not act as a voltage regulator.
