Question

In the given circuit, the resistance of the conductor which is connected in form of ring is zero, then the resultant resistance across A, B is

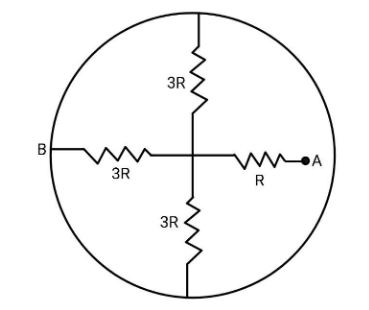
(A) $2R$
(B) $4R$
(C) $7R$
(D) $10R$

Answer 1

Here, you are asked to find the equivalent resistance in between the points A and B. A circuit might look complicated but in most of the cases you can actually reduce the circuit, meaning that if the circuit has a $n$ number of resistors, it might be possible for you to reduce the number of resistances. The way to reduce is to find combinations of resistances, whether they are connected in series or parallel. In order to proceed, find the series and parallel combinations in the given figure and reduce the circuit accordingly.

Complete step by step answer:
In order to find whether the resistances are connected in series or parallel, you look for the ends of each resistances. Consider the four ends of two resistors ${R_1}\& {R_2}$. If two ends, one end of ${R_1}$ and the other end of ${R_2}$ are connected to each other, we say that the resistors are connected in series. If both the ends of both the resistors are connected to each other as a pair, we say that the resistors are connected in parallel.

In other words, if resistors are in series, the same amount of current will flow through each resistor and if they are in parallel, the potential across each resistor will be the same. You will get an idea of this as we will discuss the above question.Consider the above combination of resistors. It is given that the resistance of the conductor is zero. If you consider any two points on this conductor, as there is zero resistance, these two points will be at the same potential.

So, all the points on the conductor are at the same potential, say ${V_C}$. Let the potential of the point where the $3R$ resistances meet be ${V_O}$. If you observe carefully, potential difference across all the $3R$ resistors is equal to ${V_C} - {V_O}$, therefore, the $3R$ resistances are connected in parallel. The equivalent resistance of parallel combination will be,
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{3R}} + \dfrac{1}{{3R}} + \dfrac{1}{{3R}} \\\ \Rightarrow\dfrac{1}{{{R_p}}} = \dfrac{3}{{3R}} \\\ \Rightarrow {R_p} = R$.

Now, observe the next resistance $R$, you can see that they have only one point in common which is the centre one having potential ${V_O}$, so, the resistances ${R_p}$(the equivalent of the three $3R$ resistors) and $R$ are in series. As they are in series, the resultant resistance will be the sum of resistances. Therefore,
${R_{resultant}} = {R_p} + R \\\ \Rightarrow{R_{resultant}} = R + R \\\ \therefore{R_{resultant}} = 2R$
Hence, the resultant resistance across A, B is $2R$.

Hence, option A is correct.

Note: Always remember that whenever two resistors are having only a single common point, they are connected in series and when $n$ number of resistors are having two points in common, they are connected in parallel. Note that in case of series, only two resistors are considered. There may be an $n$ number of resistors connected in series but you take any two of them and they will have only one common point. Also note that we have considered that current is flowing in the circuit.