Question
Question: In the given circuit, the potential difference between A and B is 18 V, and the charge on the 2 \(\m...
In the given circuit, the potential difference between A and B is 18 V, and the charge on the 2 μF capacitor is 24μC. The value of C is:
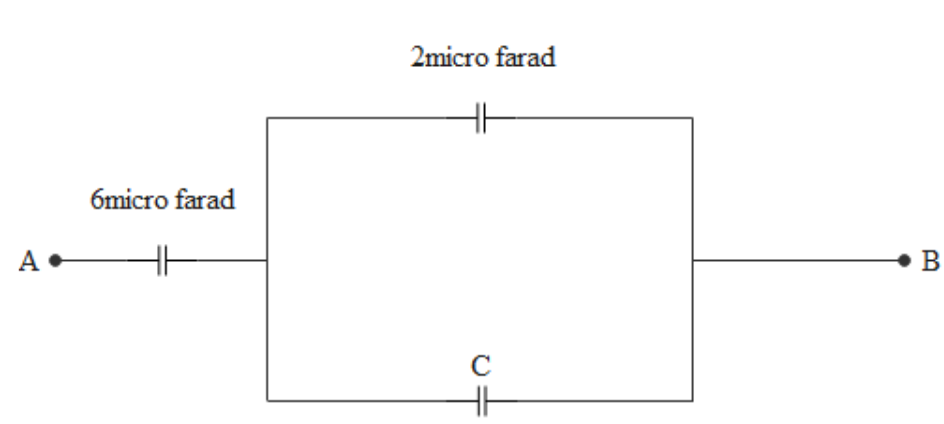
A. 1 μF
B. 2 μF
C. 3 μF
D. 4 μF
Solution
Capacitor is a device which is used to store the charge. The charge stored in the capacitor depends on the potential difference applied across them and also depends on the capacitance of the capacitor. We will use the relation between them to solve this question.
Formula used:
q=cV
Complete step-by-step solution:
Generally, when there is more than one capacitor, we can connect them in series or we can connect them in parallel.
In the case of series connection, the current flowing through the circuit will be the same which means that the charge stored on every capacitor will be the same as the charge is nothing but the current flowing in the given time.
In the case of parallel connection, the voltage across all the capacitors will be the same and then we can calculate the charge on each capacitor from that voltage.
In a series connection charge will be the same and the voltage will be divided across the capacitors whereas in a parallel connection voltage will be the same and the charge will be divided across the capacitors.
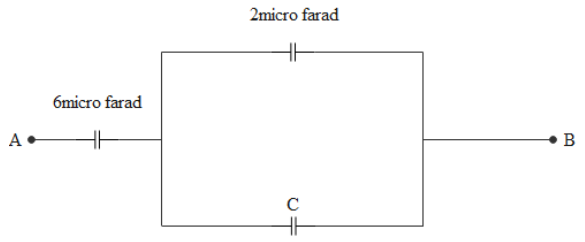
The charge stored across a capacitor is given as q=cV where ‘c’ is the capacitance and ‘V’ is the voltage across it.
In case of 2 micro farad capacitor since charge across it is 24 micro coulombs voltage across it will be
q=cV
\eqalign{
& \Rightarrow 24 = 2V \cr
& \Rightarrow V = \dfrac{{24}}{2} \cr
& \Rightarrow V = 12{\text{volts}} \cr}
capacitor C and 2 micro farad capacitor are in parallel connection, so voltage across C also will be 12 volts
Total potential difference between points A and B is 18 volts out of which 12 volts is across capacitor C and 2 micro farad capacitor and the remaining is 6 volts and this will be across 6 micro farad capacitor
So charge on 6 microfarad capacitor is
q=cV
\eqalign{
& \Rightarrow q = 6 \times 6 \cr
& \Rightarrow q = 36\mu C \cr}
Out of 36 micro coulombs 2 micro farad capacitor has 24 micro coulombs. So the remaining will be 36−24=12μC
Hence 12μC will be on capacitor ‘C’ and voltage across capacitor ‘C’ IS 12 volts.
So capacitance of capacitor ‘C’ will be
q=cV
\eqalign{
& \Rightarrow c = \dfrac{q}{V} \cr
& \Rightarrow c = \dfrac{{12\mu C}}{{12V}} \cr
& \Rightarrow c = 1\mu F \cr}
Hence option A will be the answer
Note: The formulas which we have for the case of finding effective capacitance of parallel and series connection of capacitors will be exactly opposite to the case of finding effective resistance of parallel and series connection of resistors. The given question can also be solved by finding effective capacitance and then voltage distribution and then finding charge and equating the charge to the given value.
