Question
Question: In the given circuit, the potential difference across \(3\mu F\) capacitor will be: A) 16 V B) 1...
In the given circuit, the potential difference across 3μF capacitor will be:
A) 16 V
B) 10 V
C) 6 V
D) 4 V
Solution
Kirchhoff’s first law states the total current entering a junction or a node is equal to the charge leaving the node as no charge is lost. In order to find the solution of the given question apply Kirchhoff’s first law along the given circuit.
Formula used:
ΣI=0
Complete answer:
Kirchhoff’s first law also known as the current law is given as the sum of the current entering in a junction is equal to the sum of the current leaving the junction.
Mathematically, it is given as
ΣI=0 ; where I is denoted as the current in the circuit.
The second law of Kirchhoff’s states that the algebraic sum of all the voltages around any closed loop in a circuit is equal to zero for a closed loop series path.
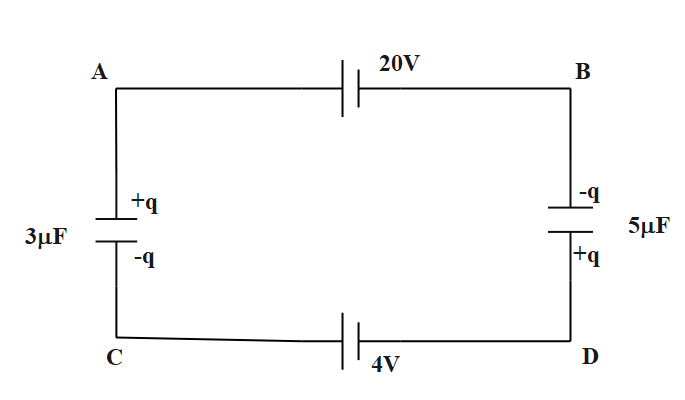
Using Kirchhoff’s voltage law in the loop ABCDA,
⇒3q+4+5q−20=0
⇒3q+5q=20−4
⇒15(5q+3q)=16
⇒8q=15×16
⇒q=8(15×16)=30μC
∣VA−VB∣=3q=330=10Volt
So, the correct answer is “Option B”.
Additional Information:
Kirchhoff’s law is also known as the conservation of energy, as moving around a closed loop, or a circuit, we will end up back to where we started in the circuit and thus back to the same initial potential with no loss of voltage around the loop. Therefore, any voltage drops around the loop must be equal to any voltage sources met along the way.
Note:
It is important to pay special attention to the algebraic signs of the voltage drops across the elements and the emf’s of the source, while applying Kirchhoff’s law to a specific circuit element as there are chances of making mistakes in the calculations.
