Question

In the given circuit the internal resistance of the 18 V cell is negligible. If the${R_1} =400\Omega$, ${R_3} = 100\Omega$ and ${R_4} = 500\Omega$ and the reading of an ideal voltmeter across ${R_4}$is 5V, then the value ${R_2}$will be

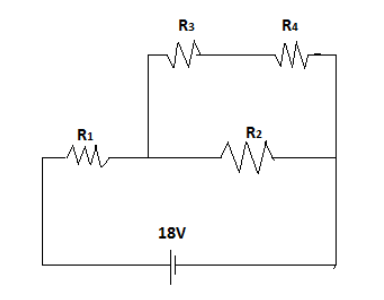
A. 300Ω
B. 230Ω
C. 450Ω
D. 550Ω

Answer 1

In this question the value of voltage across the resistance ${R_4}$is given so by using ohm's law $V = IR$, find the current through the resistance ${R_4}$which is same as current through $R_3$ the we will find the current through resistance $R_1$and then find the current through the resistance ${R_2}$whose resistance will be calculated.

Step by step answer: ${R_1} = 400\Omega$
${R_3} = 100\Omega$
${R_4} = 500\Omega$
The voltage across the resistance ${R_4}$ is $= 5V$
Now we can redraw the given circuit as

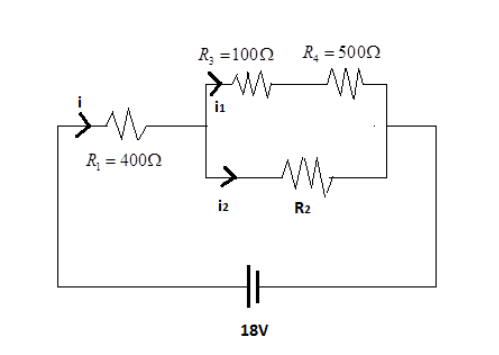
Where current i is flowing through the resistance $R_1$ which further divides into current $i_1$ and $i_2$, where current $i_1$ flows through the resistances $R_3$ and $R_4$ whereas current $i_2$ flows through the resistance $R_2$,
Now consider the resistance $R_4$ Where the voltage across through it is 5V, hence the current
${i_1} = \dfrac{{{V_4}}}{{{R_4}}} = \dfrac{5}{{500}} = 0.01A$
We know that the current flowing through the resistances in the series is equal, hence we can say the current through the resistance $R_3$ will be$0.01A$, so the voltage across the resistance $R_3$ will be
${V_3} = {i_1}{R_3} = 0.01 \times 100 = 1V$
So the voltage across the resistances $R_3$ and $R_4$ will be
$V = {V_3} + {V_4} = 1 + 5 = 6V$
Now we know that when resistances are connected in series then the voltage across them is equal, hence we can say voltage across the resistances ${R_2}$will be same as the voltage across the resistances $R_3$ and $R_4$, hence we can write
$V = {V_2} = 6V$
From the circuit we can see the resistance $R_1$ is in series with the parallel combination of resistances $R_2$, $R_3$ and $R_4$ and the voltage across the whole circuit is 18v, hence we can write
${V_1} + V = 18V$
Hence by substituting the value of voltage$V = 6V$, we can write

$$\Rightarrow {V_1} + V = 18V \\\ \Rightarrow {V_1} = 18 - V \\\ \Rightarrow {V_1} = 18 - 6 \\\ \Rightarrow {V_1 }= 12V \\\$$

So the current I through the resistance${R_1} = 400\Omega$ will be equal to
$i = \dfrac{{{V_1}}}{{{R_1}}} = \dfrac{{12}}{{400}} = 0.3A$
In this circuit since$i = {i_1} + {i_2}$, hence we can write

$$\Rightarrow {i_2} = i - {i_1} \\\ \Rightarrow {i_2} = 0.03 - 0.01 \\\ \Rightarrow {i_2} = 0.02A \\\$$

Therefore the Resistance of the resistor ${R_2}$ will be equal to
${R_2} = \dfrac{V}{{{i_2}}} = \dfrac{6}{{0.02}} = 300\Omega$

Hence the value ${R_2}$will be $= 300\Omega$ Option A is correct.

Note: In these types of questions, students need to be very careful while deciding for the parallel and the series connection of the resistances. The resistances (or combination of resistances) across which the voltage is same, then the resistances are known to be parallel connected whereas the resistances through which the amount of flow of current is the same then, they are known as series connected. It is not always necessary for the resistances to be connected in series or in parallel