Solveeit Logo
Login

Question

Question: In the given circuit the current \({I_1}\) (magnitude only) is: ![](https://www.vedantu.com/questi...

In the given circuit the current I1{I_1} (magnitude only) is:

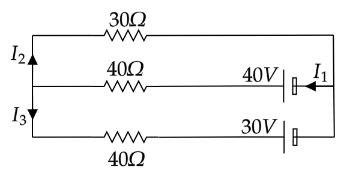
A. 0.4 A0.4\,A
B. 0.7 A0.7\,A
C. 0.8 A0.8\,A
D. None of these

Explanation

Solution

Use the Kirchhoff’s laws to solve the circuit problem. Kirchhoff’s current law states that the algebraic sum of the currents meeting at a junction in an electrical circuit is zero.

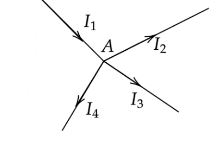
According to Kirchhoff’s Current law at the junction A in the above diagram,
−I1+I2+I3+I4=0- {I_1} + {I_2} + {I_3} + {I_4} = 0
⇒I1=I2+I3+I4\Rightarrow {I_1} = {I_2} + {I_3} + {I_4}
The algebraic sum of incoming currents is equal to algebraic the sum of outgoing currents. Kirchhoff’s voltage law states that in any electrical circuit loop, the algebraic sum of all the electromotive forces and the voltage drops in resistors is equal to zero

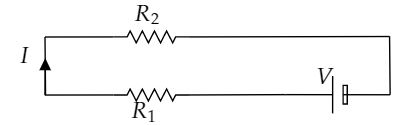
Apply Kirchhoff's voltage law in the above loop.
−IR1−IR2+V=0- I{R_1} - I{R_2} + V = 0
⇒V=IR1+IR2\Rightarrow V = I{R_1} + I{R_2}
The algebraic sum of all electromotive forces is equal to the algebraic sum of voltage drops across the resistors.

Complete step by step answer:
Let’s redraw the given diagram

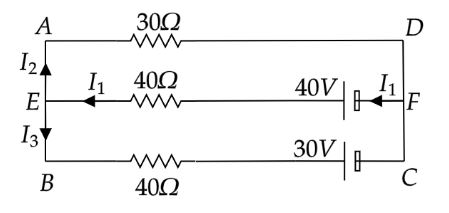
Apply Kirchhoff's Current law at the junction EE in the above circuit diagram.
I1=I2+I3{I_1} = {I_2} + {I_3}
Now apply Kirchhoff’s voltage law in the loop AEFDAEFD.
40I1+30I2=4040{I_1} + 30{I_2} = 40
4I1+3I2=44{I_1} + 3{I_2} = 4 …… (1)
Apply Kirchhoff’s voltage law in the loop EBCFEBCF.
40I1+40I3=40−3040{I_1} + 40{I_3} = 40 - 30

Now substitute I3=I1−I2{I_3} = {I_1} - {I_2} in the above equation.
4I1+4(I1−I2)=14{I_1} + 4\left( {{I_1} - {I_2}} \right) = 1
⇒8I1−4I2=1\Rightarrow 8{I_1} - 4{I_2} = 1
Further simplifying in terms of I1{I_1}
⇒I2=2I1\Rightarrow {I_2} = 2{I_1}
Substitute the value of I2{I_2} in the above equation (1).
4I1+3(2I1)=44{I_1} + 3\left( {2{I_1}} \right) = 4
Further calculating
10I1=410{I_1} = 4
∴I1=0.4 A\therefore {I_1} = 0.4\,A

Hence, the correct option is (A)\left( A \right).

Note: While applying the Kirchhoff’s voltage law to a closed, algebraic sums are considered. Therefore, it is very important to assign proper signs to electromotive forces (e.m.f.) and voltage drops in the loop. A rise in potential should be considered positive and fall in potential should be considered as negative.