Question

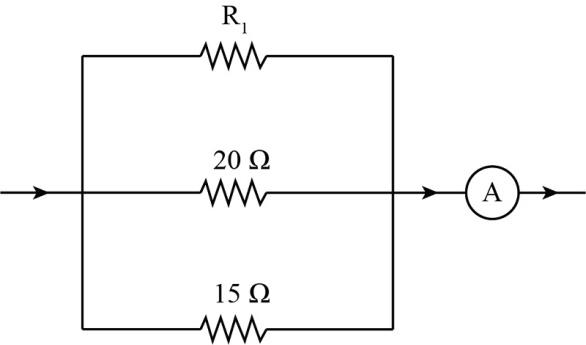
-In the given circuit the current flowing through the resistance is $20\;{\rm{ohms}}$ is $0.3\;{\rm{ampere}}$ while the ammeter reads $0.8\;{\rm{ampere}}$. What is the value of ${R_1}$ in ohms?

Answer 1

Here, first we analyze the circuit and then approaches to next step. The voltage through the $20\;{\rm{ohms}}$ resistance is equal to the voltage across the circuit. It gives us the equivalent resistance of the circuit. We can see that the all three resistances are in parallel with each other. Then we will use the formula for resistances in parallel to find the value of resistance ${R_1}$.

Complete step by step answer:
Given: We have three resistances in the given circuit. The resistances are ${R_2} = 20\;{\rm{ohms}}$ , ${R_3} = 15\;{\rm{ohms}}$ and ${R_1}$. The current flowing through the resistance of ${R_2} = 20\;{\rm{ohms}}$ is ${I_2} = 0.3\;{\rm{ampere}}$. The total current in the ammeter is $I = 0.8\;{\rm{ampere}}$.
The current through the ammeter is given, the potential across the ammeter will be equal to the voltage across ${R_2} = 20\;{\rm{ohms}}$ resistance because all three resistance are in parallel with each other.
${V_2} = V$
Here, V is the potential across the ammeter and ${V_2}$ is the potential across the resistance of 20 ohms.
${I_2}{R_2} = {R_{eq}}I$
Here, ${R_{eq}}$ is the equivalent resistance of the circuit.
We substitute the values in above relation,
$0.3 \times 20 = {R_{eq}} \times 0.8\\\ \implies 6 = {R_{eq}} \times 0.8\\\ \implies {R_{eq}} = \dfrac{6}{{0.8}}\\\ \implies {R_{eq}} = \dfrac{{15}}{2}\;{\rm{ohms}}$
We write the formula for the resistance in parallel to find the resistance ${R_1}$.
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$
Now, we substitute the values in above relation,
$\dfrac{2}{{15}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{20}} + \dfrac{1}{{15}}\\\ \implies \dfrac{1}{{{R_1}}} = \dfrac{{8 - 3 - 4}}{{60}}\\\ \implies \dfrac{1}{{{R_1}}} = \dfrac{1}{{60}}$
We perform cross multiplication and multiply ${R_1}$ to 1 and 60 to 1. It gives us the value of resistance ${R_1}$.
Then, we write the obtained value of ${R_1}$.
${R_1} = 60\;{\rm{ohms}}$

Therefore, the value of resistance ${R_1}$ is $60\;{\rm{ohms}}$.

Note:
In this question, the students must have the knowledge of potential difference and knowledge of the term diode. This question can alternatively be solved by Kirchhoff's voltage law. Kirchhoff’s gives two laws, first current law and voltage law. Kirchhoff’s current law states that the summation of all the current in the circuit is equal to zero. And Kirchhoff’s voltage law states that the summation of all the voltage in the circuit is equal to zero.