Question

In the given circuit, the cells have zero internal resistance. The currents (in Amperes) passing through resistance ${R_1}$ and ${R_2}$ respectively are

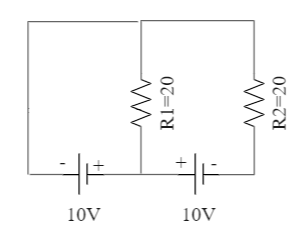
A. 2, 2
B. 0, 1
C. 1, 2
D. $0.5$, 0

Answer 1

Hint
The current through a resistor is dependent on the potential difference across it and the resistance possessed by the resistor. The potential difference across two points varies depending on the orientation of the source used.
$\Rightarrow I = \dfrac{V}{R}$, where V is the voltage across the component in consideration and R is the total resistance. I am currently in Amperes.

Complete step by step answer
Here, we have two resistances that are connected to two different voltage supplies with different orientation. We are asked to determine the current flowing through the two due to this potential difference.
We know that a cell creates a potential difference across the electrical component, and hence the voltage across the two resistances depending on the different orientation of the cell will be:

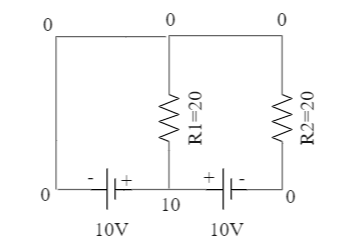
Now, we know that the current across a resistor is given by:
$\Rightarrow I = \dfrac{V}{R}$
So, for resistor ${R_1}$ we have $R = 20$ and $V = 10$ :
$\Rightarrow I = \dfrac{{10}}{{20}} = 0.5$ A
And for resistor ${R_2}$ we have $R = 20$ and $V = 0$ :
$\Rightarrow I = \dfrac{0}{{20}} = 0$ A
Hence, the correct answer is option (D): $0.5$, 0.

Note
The orientation of cells or voltage source plays an important role in current flow and potential difference across a component. For example, while trying to turn on a battery-powered charge, it will only work when the cells are correctly aligned with the positive and negative terminal of the components of the torch. When we insert the battery in an opposite direction, the current flowing across the circuit becomes 0 just as we saw for resistance 2.