Question

In the given circuit shown in the figure, each resistance is $R$. Net resistance between points $A$ and $B$ is

A. $\dfrac{4}{3}R$
B. $\dfrac{7}{2}R$
C. $\dfrac{1}{2}R$
D. $\dfrac{5}{3}R$

Answer 1

Find the equivalent resistance of the circuit using the formula for equivalent resistance of resistors connected in series and parallel circuit. For series circuit equivalent resistance is sum of all the resistances while for parallel circuit is reciprocal sum of the resistances.

Formula used:
Equivalent resistance connected in series is given by,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ...$
where ${R_1}$ ,${R_2}$… are the resistances connected in series.
The equivalent resistance in a parallel circuit is given by,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ....$
where, ${R_{eq}}$ is the equivalent resistance of the circuit and ${R_1}$ ,${R_2}$… are the resistances connected in parallel.

Complete step by step answer:
We have given here a circuit with resistances on it and we have to find the equivalent resistance of the circuit with respect to the terminals AB. Now, first let’s name the other two point CD.

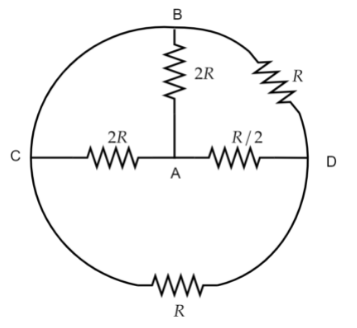
Now, the point C and B are the same point as they are joined by a wire. So, if we redraw the diagram using simpler series parallel connection we will have the circuit as follows:

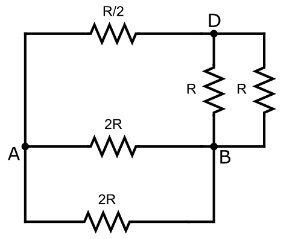
Now, there is a parallel connection between the points BD.
So, the equivalent resistance of that branch will be,
$\dfrac{{R \times R}}{{R + R}} = \dfrac{R}{2}$
Hence, the diagram can be redrawn as,

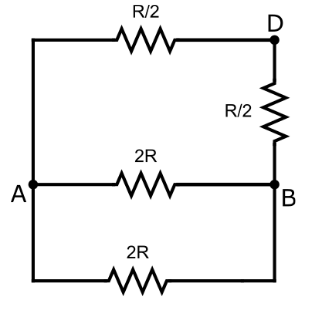
Now, both the resistances $\dfrac{R}{2}$are in series. Hence the equivalent resistance will be,
$\dfrac{R}{2} + \dfrac{R}{2} = R$
Hence, the circuit can be drawn again as:

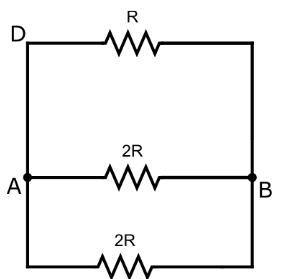
Now, these three resistance are in parallel connection in between AB.
So, the equivalent resistance between AB will be,
$\dfrac{1}{{{R_{AB}}}} = \dfrac{1}{R} + \dfrac{1}{{2R}} + \dfrac{1}{{2R}}$
$\Rightarrow \dfrac{1}{{{R_{AB}}}} = \dfrac{{2 + 1 + 1}}{{2R}}$
$\Rightarrow \dfrac{1}{{{R_{AB}}}} = \dfrac{4}{{2R}}$
$\therefore {R_{AB}} = \dfrac{R}{2}$
Hence, the equivalent resistance of the circuit between $AB$ will be $\dfrac{R}{2}$.

Hence, option C is the correct answer.

Note: Please notice that when redrawing the circuit the connection between the C and D point is short. Hence these two points are the same points in the circuit. If those points are not short then the equivalent resistance of the circuit will be completely different.Also, always remember that the parallel connection only occurs when resistances are joined between the same points.