Solveeit Logo
Login

Question

Question: In the given circuit, $R_1 = 1 \ \Omega$, $R_2 = 2 \ \Omega$, $R_3 = 2 \ \Omega$, $R_4 = 1 \ \Omega$...

In the given circuit, R1=1 ΩR_1 = 1 \ \Omega, R2=2 ΩR_2 = 2 \ \Omega, R3=2 ΩR_3 = 2 \ \Omega, R4=1 ΩR_4 = 1 \ \Omega, r=23 Ωr = \frac{2}{3} \ \Omega and ε=10 V\varepsilon = 10 \ V. Find the:

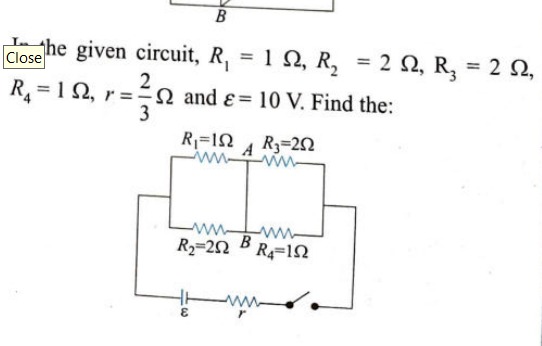
A

Total current from the battery and the potential difference between points A and B

B

Equivalent resistance of the circuit and the total current

C

Potential difference across R3 and R4

D

Current through R1 and R2

Answer

Total current from the battery: 6013 A\frac{60}{13} \ A, Potential difference between A and B (VABV_{AB}): 3013 V\frac{30}{13} \ V

Explanation

Solution

  1. Calculate the equivalent resistance of the top branch (Rtop=R1+R3=1 Ω+2 Ω=3 ΩR_{top} = R_1 + R_3 = 1 \ \Omega + 2 \ \Omega = 3 \ \Omega) and the bottom branch (Rbottom=R2+R4=2 Ω+1 Ω=3 ΩR_{bottom} = R_2 + R_4 = 2 \ \Omega + 1 \ \Omega = 3 \ \Omega).
  2. Calculate the equivalent resistance of the parallel combination (Rparallel=Rtop×RbottomRtop+Rbottom=3×33+3=96=32 ΩR_{parallel} = \frac{R_{top} \times R_{bottom}}{R_{top} + R_{bottom}} = \frac{3 \times 3}{3 + 3} = \frac{9}{6} = \frac{3}{2} \ \Omega).
  3. Calculate the total resistance of the circuit, including the internal resistance (Rtotal=Rparallel+r=32 Ω+23 Ω=96+46=136 ΩR_{total} = R_{parallel} + r = \frac{3}{2} \ \Omega + \frac{2}{3} \ \Omega = \frac{9}{6} + \frac{4}{6} = \frac{13}{6} \ \Omega).
  4. Calculate the total current drawn from the battery using Ohm's Law (I=εRtotal=10 V136 Ω=6013 AI = \frac{\varepsilon}{R_{total}} = \frac{10 \ V}{\frac{13}{6} \ \Omega} = \frac{60}{13} \ A).
  5. Since the parallel branches have equal resistance, the total current splits equally (Itop=Ibottom=I2=3013 AI_{top} = I_{bottom} = \frac{I}{2} = \frac{30}{13} \ A).
  6. Calculate the potential at Node X (after internal resistance): VX=ε−I×r=10 V−6013 A×23 Ω=10−4013=9013 VV_X = \varepsilon - I \times r = 10 \ V - \frac{60}{13} \ A \times \frac{2}{3} \ \Omega = 10 - \frac{40}{13} = \frac{90}{13} \ V.
  7. Calculate the potential at point A: VA=VX−Itop×R1=9013 V−3013 A×1 Ω=6013 VV_A = V_X - I_{top} \times R_1 = \frac{90}{13} \ V - \frac{30}{13} \ A \times 1 \ \Omega = \frac{60}{13} \ V.
  8. Calculate the potential at point B: VB=VX−Ibottom×R2=9013 V−3013 A×2 Ω=9013−6013=3013 VV_B = V_X - I_{bottom} \times R_2 = \frac{90}{13} \ V - \frac{30}{13} \ A \times 2 \ \Omega = \frac{90}{13} - \frac{60}{13} = \frac{30}{13} \ V.
  9. Calculate the potential difference between A and B: VAB=VA−VB=6013 V−3013 V=3013 VV_{AB} = V_A - V_B = \frac{60}{13} \ V - \frac{30}{13} \ V = \frac{30}{13} \ V.