Question

In the given circuit find the current through the Zener diode.

(A) 2.5 mA
(B) 3.3 mA
(C) 5.5 mA
(D) 6.7 mA

Answer 1

Draw the circuit and show the current in the circuit and apply Kirchhoff’s current law in the circuit. According to Kirchhoff’s current law, the algebraic sum of the currents flowing through a junction is zero. After applying Kirchhoff’s law we found that the current in the Zener diode is the difference of current passing through both resistors.

Complete step by step answer:
Given:
The voltage of the circuit is ${V_1} = 15\;{\text{V}}$.
The voltage of the zener diode is ${V_2} = 10\;{\text{V}}$.
The value of first resistance is ${R_1} = 500\;{{\Omega }}$.
The value of second resistance is ${R_2} = 1500\;{{\Omega }}$.

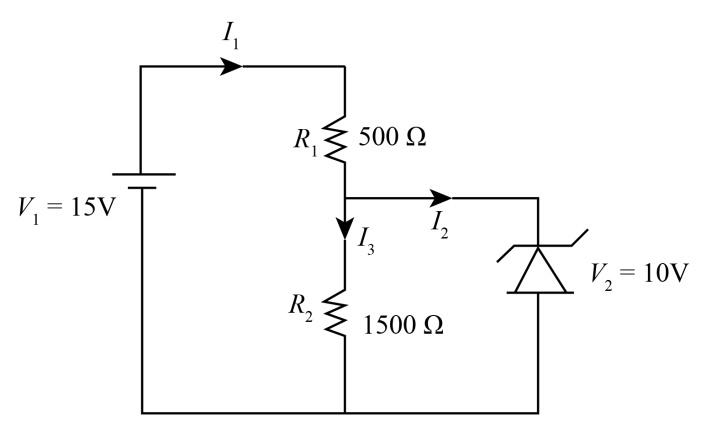
Apply Kirchhoff’s current law in the above circuit
$I_1 - I_2 - I_3 = 0$ .......................(1)
The expression to calculate ${I_2}$ is
$I_2 = \dfrac{{{V_2}}}{{{R_2}}}$ ......................(2)
Substituting $10\;{\text{V}}$ for ${V_2}$, and $1500\;{{\Omega }}$ for ${R_2}$ in (2), to find the value of ${I_2}$.
$\Rightarrow {I_2} = \dfrac{{10\;{\text{V}}}}{{1500\;{{\Omega }}}}$
$\Rightarrow {I_2} = \dfrac{1}{{150}}\;{\text{A}}$.....................(3)
The expression to calculate ${I_1}$ is:
$\Rightarrow {I_1} = \dfrac{{{V_1} - {V_2}}}{{{R_1}}}$ ................(4)
Substituting, $10\;{\text{V}}$ for ${V_2}$, $15\;{\text{V}}$ for ${V_1}$ and $500\;{{\Omega }}$ for ${R_1}$ in (4), to find the value of ${I_1}$.
$\Rightarrow I_1 = \dfrac{{15\;{\text{V - 10}}\;{\text{V}}}}{{500\;{{\Omega }}}}$
$\Rightarrow I_1 = \dfrac{1}{{100}}\;{\text{A}}$................... (5)
From equation (1), (3) and (5)
$\Rightarrow \left( {\dfrac{1}{{100}}\;{\text{A}}} \right) - \left( {\dfrac{1}{{150}}\;{\text{A}}} \right){\text{ - }}\left( {{{\text{I}}_3}} \right) = 0 \\\ \Rightarrow {I_3} = \dfrac{1}{{300}}\;{\text{A}} \\\ \Rightarrow {I_3} = 0.003\;{\text{A}} \times \dfrac{{1000\;{\text{mA}}}}{{1\;{\text{A}}}} \\\ \Rightarrow {{\text{I}}_3} = 3.3\;{\text{mA}} \\\$
As shown in diagram ${I_3}$ the current passes through Zener diodes. So, the current passes through the Zener diode is $3.3\;{\text{mA}}$.

Additional Information:
In a Zener diode, current flows in reverse as well as forward direction when the voltage exceeds break down voltage. This breakdown voltage is known as Zener voltage. Zener diodes are widely used as voltage regulators. Zener diode is also used to limit the current through the diode and drop the excess voltage in the conducting diode.

Note:
Zener diode is the special diode which works in reverse biased and breakdown regions. Zener diodes are used as voltage regulators. When a Zener diode is connected in forward bias then its characteristics are just the same as ordinary diodes.