Question

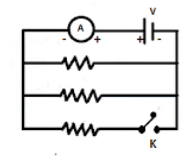
In the given circuit diagram, the cell and the ammeter, both have negligible resistances. The resistances are identical. With the switch $K$ open, the ammeter reads $0.6A$ . What will be the ammeter reading when the switch is closed?

Answer 1

Hint : In order to solve this question, we are going to first consider the case where the switch $K$ is open and by using the information given, we can easily determine the voltage. Now as the voltage remains the same, thus, from that, we will find the value of current for when the switch is closed.
Formula used: The formula for the equivalent resistance of the resistors $R$ connected in parallel is
$\dfrac{1}{{{R_1}}} = \dfrac{1}{R} + \dfrac{1}{R}$

Complete Step By Step Answer:
Let us consider that the resistances of each resistor is $R$ .
In the case where the switch $K$ is open, then, the circuit has only two resistances that are in parallel, and the ammeter reading is $0.6A$ .
The equivalent resistance in this case is
\dfrac{1}{{{R_1}}} = \dfrac{1}{R} + \dfrac{1}{R} = \dfrac{2}{R} \\\ \Rightarrow {R_1} = \dfrac{R}{2} \\\
Let the potential difference of the cell be $V$
Current $I = 0.6A$
$\Rightarrow V = I{R_1} = 0.6 \times \dfrac{R}{2} = 0.3R$

Now when the key ‘k’ is closed, all three resistances are parallel in the circuit. Therefore,

The relation for the equivalent resistance of these three resistors can be written as:
\dfrac{1}{{{R_2}}} = \dfrac{1}{R} + \dfrac{1}{R} + \dfrac{1}{R} = \dfrac{3}{R} \\\ \Rightarrow {R_2} = \dfrac{R}{3} \\\
Using the Ohm’s law, we get
\Rightarrow V = I{R_2} = I \times \dfrac{R}{3} \\\ \Rightarrow 0.3R = \dfrac{{IR}}{3} \\\ \Rightarrow I = 0.9A \\\
Therefore, the ammeter reads $0.9A$ .

Note :
When a switch in the circuit is open, this makes that element or the wire disconnected from the circuit and the only elements that lie in this closed circuit are those that are directly connected to the battery and the ammeter, while when it is closed, it completes the whole circuit, taking that section also in the circuit.