Question: In the given circuit diagram power consumption is maximum then ratio of readings of voltmeters \({V_...

Question

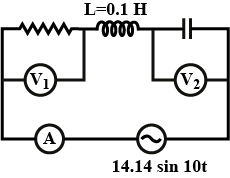
In the given circuit diagram power consumption is maximum then ratio of readings of voltmeters ${V_1}$ and ${V_2}$ ( Reading of ammeter is $2\;{\text{A}}$ ):

(A) $\dfrac{1}{5}$
(B) $5$
(C) $1$
(D) Data insufficient

Answer 1

Solution

Hint:- The impedance of the LCR circuit depends on the capacitive reactance and inductive reactance. For finding those values, we need the values of inductance and capacitance. Check whether those are given. And the power consumed depends on the current through the circuit.

Complete step by step solution:
In LCR circuits, the expression for the inductive reactance is given as,
${X_L} = \omega L$
Where, $\omega$ is the angular frequency and $L$ is the conductance.
And the expression for the capacitive reactance is given as,
${X_C} = \dfrac{1}{{\omega C}}$
Where, $C$ is the capacitance.
We have given the inductance as $L = 0.1\;{\text{H}}$ .
Therefore, ${X_L} - {X_C} = \omega L - \dfrac{1}{{\omega C}}$
Substitute the given value.
${X_L} - {X_C} = 0.1\omega - \dfrac{1}{{\omega C}}$
The value of capacitance is not given.
The expression for the impedance in the LCR circuit is given as,
$Z = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}}$
Where, $R$ is the resistance of the circuit. The value of $R$ is not given.
From the figure, $V\sin \omega t = 14.14\sin 10t$
Thus the voltage across the circuit is $14.14$ .
For the power consumption, we have to find the current flowing through the circuit.
The expression for the current in the circuit is given as,
$I = \dfrac{V}{Z}$
Substituting in the above expression,
$I = \dfrac{{14.14}}{{\sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} }}$
The value of resistance and capacitance are not given. Hence the power consumed in this LCR circuit cannot be found.
Here the given data is insufficient to find the current in the circuit.

The answer is option D.

Note: If the question is given that the circuit is in resonance and the value of resistance is given the power consumption is easy to find. Hence the capacitive reactance and inductive reactance will be equal in resonance.