Question

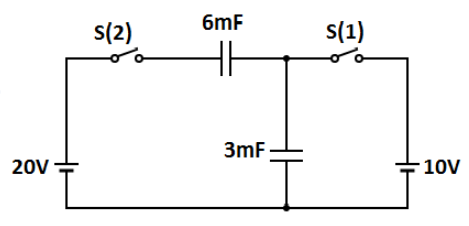
In the given circuit below, the first switch ${S_1}$ is closed and when steady state is reached the switch ${S_2}$ is also closed. Then what is the charge on the capacitor shown in the circuit of capacitance $6\mu F$ :

Answer 1

In order to find the charge stored on capacitor of capacitance $6\mu F$ we will find the magnitude of difference of potentials between two ends of the capacitor of capacitance $6\mu F$ and then by using the relation between charge, potential difference and capacitance of a capacitor we will find the charge using $Q = CV$ .

Complete step by step answer:
Given that, As soon as switch ${S_1}$ is closed then the battery of $10V$ starts to supply current in second half of circuit and no current will pass through the $6\mu F$ side section of circuit and thus the right side of $6\mu F$ capacitor will have a negative potential of $10V$ .

Secondly, when switch ${S_2}$ is being closed at that moment no current flows in second half circuit due to steady state and hence potential on right side of capacitor $6\mu F$ remains same which is $10V$ and due to the second battery of voltage $20V$ the left side of $6\mu F$ will have a potential of positive $20\,V$.Hence, net potential difference across the capacitor of $C = 6\mu F$ will be $(20 - 10)V$ which is
$C = 6\mu F$
$\Rightarrow \text{Voltage} = 10\,V$
Using $Q = CV$ we get,
$Q = 6 \times 10$
$\therefore Q = 60\mu C$

Hence, the charge on the capacitor of capacitance $6\mu F$ is $Q = 60\mu C$.

Note: Remember that, as the steady state of a capacitor is reached no more current flows across the capacitor and their potentials remain the same. The micro coulomb is the unit of charge which is related as $1\mu C = {10^{ - 6}}C$ and similarly $1\mu F = {10^{ - 6}}F$ which is a unit of capacitance.