Question
Question: In the given circuit, an ideal voltmeter connected across the \[10\,\Omega \] resistance reads \[2\,...
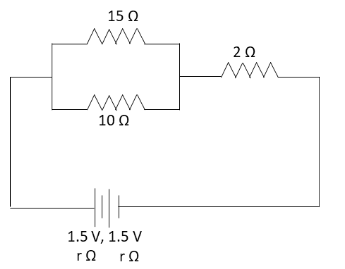
In the given circuit, an ideal voltmeter connected across the 10Ω resistance reads 2V. The internal resistance r, of each cell is:
A. 1Ω
B. 0.5Ω
C. 1.5Ω
D. 0Ω
Solution
We should use the formulae for the equivalent resistance of the two or more resistors connected in series and parallel arrangement. Also use the expression for Ohm’s law. First calculate the equivalent resistance of the two resistors connected in parallel and then calculate the equivalent resistance of all the resistors connected in the circuit. Calculate the current flowing in the circuit and use Ohm’s law to calculate the internal resistance of each cell.
Formulae used:
The equivalent resistance Req of the two resistors R1 and R2 connected in parallel is
Req1=R11+R21 …… (1)
The equivalent resistance Req of the two resistors R1 and R2 connected in series is
Req=R1+R2 …… (2)
The expression for Ohm’s law is
V=IR …… (3)
Here, V is the potential difference across the ends of the conductor, I is the electric current and R is the resistance.
Complete step by step answer:
We have given that an ideal voltmeter connected across the 10Ω resistance reads 2V.
V′=2V
Let us first calculate the equivalent resistance R′ of the two resistors connected in parallel.The equation (1) becomes
R′1=15Ω1+10Ω1
⇒R′1=15015+10
⇒R′=6Ω
Hence, the equivalent resistance of the two resistors connected in parallel is 6Ω.
Let us now draw the equivalent circuit diagram of the given circuit diagram.
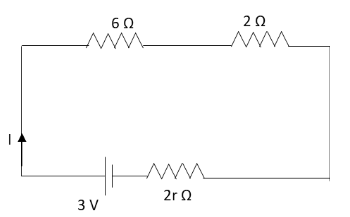
The equivalent resistance Req in the whole circuit according to equation (2) is
Req=6Ω+2Ω+2rΩ
⇒Req=(8+2r)Ω
The current flowing in the system of two parallel resistors with equivalent resistance is given by Ohm’s law.
I=R′V′
Substitute 2V for V′ and 6Ω for R′ in the above equation.
I=6Ω2V
⇒I=31A
Let now write the expression for Ohm’s law for the whole circuit.
V=IReq
Substitute 3V for V, 31A for I and (8+2r)Ω for Req in the above equation.
(3V)=(31A)[(8+2r)Ω]
⇒9=8+2r
⇒2r=1
∴r=0.5Ω
Therefore, the internal resistance of each cell is 0.5Ω.
Hence, the correct option is B.
Note: The students may think that why we have calculated the current through the system of the two resistors connected in parallel and not through the whole circuit. But the students should keep in mind that the system of two resistors in parallel is in series with the whole circuit. Hence, the net current through the system of parallel resistors will be the same through the system as the current in the series network is the same.
