Question

In the given circuit all resistances are of value R ohm each. The equivalent resistance between A and B is:

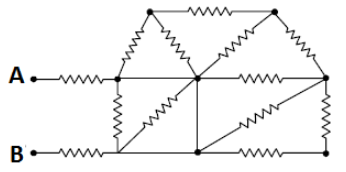
A. $2R$
B. $\dfrac{{5R}}{2}$
C. $\dfrac{{5R}}{3}$
D. $3R$

Answer 1

Here, we are asked to find the equivalent resistance between A and B. At first look of the circuit we may think that we have to solve and find the equivalent resistance of all thirteen resistances to find the answer. But, here we require to consider only two resistances to find the equivalent resistance between A and B.

Formula used:
${R_{eq}} = {R_1} + {R_2}$, where, ${R_{eq}}$ is the equivalent resistance for resistances connected in series connection, ${R_1}$ and ${R_2}$ are two resistance connected in series connection

Complete step by step answer:
Let us consider the following diagram to understand the concept of the question.

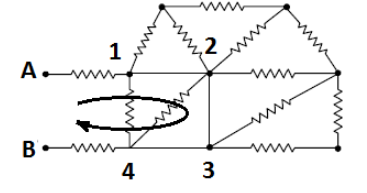
Here, we need not to solve the whole circuit of thirteen resistances to find the equivalent resistance between A and B.We will only consider four points 1, 2, 3 and 4 as shown in the figure. All the four resistances are at same potential, therefore they are short circuited. Thus, for finding the equivalent resistance between A and B, our simplified circuit becomes as shown in the following diagram.

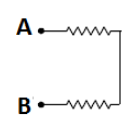
As we can see in this simplified circuit, two resistances are connected in series between A and B. It is given that each resistance is of $R\Omega$.
We know that for series connection of resistances, the equivalent resistance is given by the following formula:
${R_{eq}} = {R_1} + {R_2}$ $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
Therefore, for this case, we can say that
$\therefore{R_{eq}} = R + R = 2R$
Thus, the equivalent resistance between A and B is $2R\Omega$.

Hence, option A is the right answer.

Note: The main point to keep in mind while solving this question is not to consider all thirteen resistance to calculate required equivalent resistance between A and B. Also, here we have determined the equivalent resistance by using the formula for equivalent resistance in series connection which is ${R_{eq}} = {R_1} + {R_2}$. However, when the resistances are connected in parallel, the equivalent resistance is given by the formula $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ .