Question

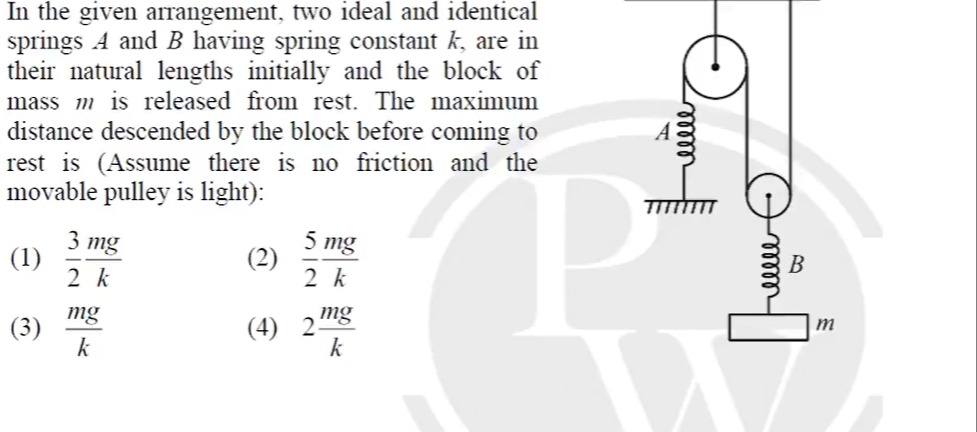
In the given arrangement, two ideal and identical springs A and B having spring constant k, are in their natural lengths initially and the block of mass m is released from rest. The maximum distance descended by the block before coming to rest is (Assume there is no friction and the movable pulley is light):

• A. $\frac{3}{2}\frac{mg}{k}$
• B. $\frac{5}{2}\frac{mg}{k}$
• C. $\frac{mg}{k}$
• D. $2\frac{mg}{k}$

Answer 1

Answer: (D)

$2\frac{mg}{k}$

Answer 2

The problem is solved using conservation of energy. Let $y$ be the maximum downward displacement of the block and $y_p$ be the downward displacement of the movable pulley. The extensions of springs B and A are $x_B = y - y_p$ and $x_A = y_p$, respectively. Thus, $y = x_A + x_B$. By analyzing the forces on the movable pulley, we find that at the maximum displacement (where velocity is zero), the net force on the pulley is zero, which implies $kx_A = 0$, so $x_A = 0$. This means spring A remains at its natural length at the maximum descent. Consequently, $y = x_B$. Applying conservation of energy: Initial energy (zero) = Final potential energy (gravitational + elastic). $0 = -mgy + \frac{1}{2}kx_A^2 + \frac{1}{2}kx_B^2$. Substituting $x_A=0$ and $y=x_B$, we get $0 = -mgy + \frac{1}{2}ky^2$. Solving for $y$ gives $y = \frac{2mg}{k}$.