Question

In the given arrangement, for the system to remain under equilibrium, the ‘$\theta$’ should be

A. ${0^{\text{o}}}$
B. ${30^{\text{o}}}$
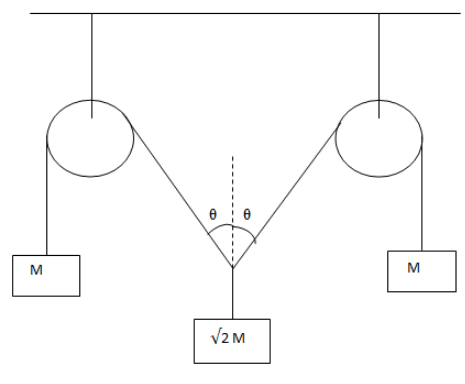
C. ${45^{\text{o}}}$
D. ${60^{\text{o}}}$

Answer 1

We are asked to find the value of angle $\theta$ when the system remains under equilibrium condition. By equilibrium it means the net force on the system is zero. First draw a free body diagram for the problem and balance the forces to find the value of $\theta$.

Complete step by step answer:
Given a system and it is asked to find the value of $\theta$ when the system is under equilibrium.When a system is in equilibrium position it means the net force on the system is zero or acceleration is zero.Let us draw a free body diagram for the system.

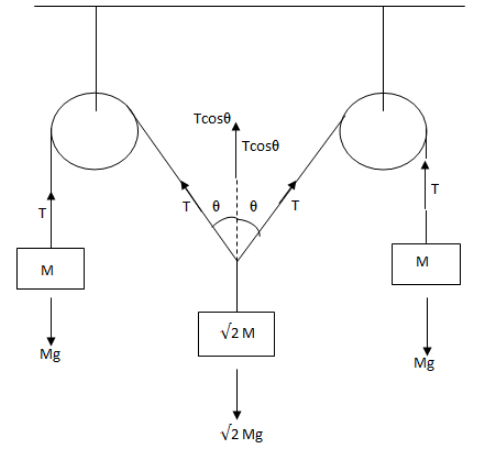
In the diagram above $T$ represents the tension on the string and $g$ is the acceleration due to gravity.
Now, balancing the forces for mass $M$ we get,
$T = Mg$ (i)
Balancing the forces for mass $\sqrt 2 M$ we get,
$T\cos \theta + T\cos \theta = \sqrt 2 Mg$
$\Rightarrow 2T\cos \theta = \sqrt 2 Mg$
Putting the value of $T$ in equation (i) we get,
$2Mg\cos \theta = \sqrt 2 Mg$
$\Rightarrow 2\cos \theta = \sqrt 2$
$\Rightarrow \cos \theta = \dfrac{{\sqrt 2 }}{2}$
$\Rightarrow \cos \theta = \dfrac{1}{{\sqrt 2 }}$
$\Rightarrow \theta = {\cos ^{ - 1}}\dfrac{1}{{\sqrt 2 }}$
$\therefore \theta = {45^{\text{o}}}$

Therefore, the value of $\theta$ when the system remains under equilibrium is ${45^{\text{o}}}$.

Note: Remember, a system is under equilibrium condition means there is no change in the state of the system. Also, for such types of questions first draw a free body diagram and then proceed for solving the question. A free body diagram is a diagram showing the forces acting on a system with their magnitudes and directions. After drawing a free body diagram, balance the forces to form equations and solve to get the required answer.