Question
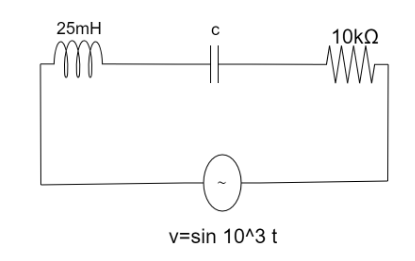
Question: In the given ac circuit capacitance is adjustable, for what value of \( c \) , the current amplitude...
In the given ac circuit capacitance is adjustable, for what value of c , the current amplitude is maximized?
(A) 4nF
(B) 40nF
(C) 4μF
(D) 40μF
Solution
Hint : We can see that the given ac circuit is an RLC circuit. In an RLC circuit, the maximum amplitude of the current is during resonance. At resonance the inductive reactance and capacitive reactance are equal. Finding the values of both the reactance and equating them we can find the value of capacitance at which this is possible.
Formula used: Inductive reactance XL=ωL
Here, inductance is represented by L , Angular frequency is represented by ω
Capacitive reactance is represented by Xc=ωc1
Capacitance is represented by c , Angular frequency is represented by ω .
Complete step by step answer
We know that at resonance in an RLC circuit the impedance is minimum and the amplitude of the current is maximum. At this condition inductive reactance and capacitive reactance are equal.
From the question voltage is equal to v=100sin103t
The general formula of voltage is v=vosinωt
Here ω is the angular frequency 103
We now know that angular frequency in the given ac circuit is 103
Inductive reactance is equal to
⇒XL=ωL
⇒XL=103×25×10−3=25
Capacitive reactance is equal to
⇒Xc=ωc1
⇒Xc=103×c1
At resonance inductive reactance and capacitive reactance are equal.
⇒Xc=XL
⇒103×c1=25
Solving for capacitance we get
⇒c1=25×103
⇒c=25×1031=40×10−6=40μF
Hence the value of capacitance is 40μF
Option (D) 40μF is the correct answer .
Note
We can say that the amplitude of the current is maximized during resonance because at resonance the impedance of the circuit is minimum which means the current is maximum. Because the current is alternating current we can say that at maximum current the amplitude will be maximum. The units of capacitance are Farad. The frequency of current and voltage at which resonance takes place is called resonant frequency.
