Question

In the following velocity time graph of a body the distance traveled by the body and its displacement during 5 seconds in meter will be

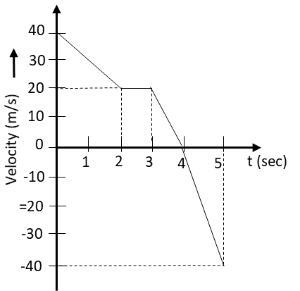
A. $75, 75$
B. $110, 70$
C. $110, 110$
D. $110, 40$

Answer 1

Determine the total area under the curve. The area under the velocity time graph of an object gives the displacement of the object. But the total sum of the area above and under the time axis or x-axis gives the total distance traveled by the object and the resultant of the sum of area above the time axis and difference of area below the time axis gives displacement of the object.

Complete step by step answer:
We know that the distance traveled by the body can be determined by taking the sum of the total area under the velocity time graph of the body. Let us name the areas under the above velocity time graph as follows:

Hence, the total distance traveled by the body in 5 seconds is the sum of the 5 areas under the given velocity time graph of the body.
${\text{Distance}} = {A_1} + {A_2} + {A_3} + {A_4} + {A_5}$
$\Rightarrow {\text{Distance}} = \left( {\dfrac{1}{2} \times 2\,{\text{s}} \times 20\,{\text{m/s}}} \right) + \left( {20\,{\text{m/s}} \times 2\,{\text{s}}} \right) + \left( {20\,{\text{m/s}} \times 1\,{\text{s}}} \right) + \left( {\dfrac{1}{2} \times 1\,{\text{s}} \times 20\,{\text{m/s}}} \right) + \left( {\dfrac{1}{2} \times 1\,{\text{s}} \times 40\,{\text{m/s}}} \right)$
$\Rightarrow {\text{Distance}} = \left( {20\,{\text{m}}} \right) + \left( {40\,{\text{m}}} \right) + \left( {20\,{\text{m}}} \right) + \left( {10\,{\text{m}}} \right) + \left( {20\,{\text{m}}} \right)$
$\therefore {\text{Distance}} = 110\,{\text{m}}$
Therefore, the distance traveled by the body in 5 seconds is $110\,{\text{m}}$.

The displacement of a body is the positive sum of the areas above the X-axis and negative sum of the areas under the x-axis of the velocity time graph of the body. Hence, the displacement of the body in 5 seconds is
${\text{Displacement}} = {A_1} + {A_2} + {A_3} + {A_4} - {A_5}$
$\Rightarrow {\text{Displacement}} = \left( {\dfrac{1}{2} \times 2\,{\text{s}} \times 20\,{\text{m/s}}} \right) + \left( {20\,{\text{m/s}} \times 2\,{\text{s}}} \right) + \left( {20\,{\text{m/s}} \times 1\,{\text{s}}} \right) + \left( {\dfrac{1}{2} \times 1\,{\text{s}} \times 20\,{\text{m/s}}} \right) - \left( {\dfrac{1}{2} \times 1\,{\text{s}} \times 40\,{\text{m/s}}} \right)$
$\Rightarrow {\text{Displacement}} = \left( {20\,{\text{m}}} \right) + \left( {40\,{\text{m}}} \right) + \left( {20\,{\text{m}}} \right) + \left( {10\,{\text{m}}} \right) - \left( {20\,{\text{m}}} \right)$
$\therefore {\text{Displacement}} = 70\,{\text{m}}$
Therefore, the displacement of the body in 5 seconds is $70\,{\text{m}}$.

Therefore, the distance travelled and displacement of the body in 5 seconds are $110\,{\text{m}}$ and $70\,{\text{m}}$ respectively. Hence, the correct option is B.

Note: In general when the velocity of the object is positive, the area under the curve is only above the time axis and we take the sum of all areas under the graph. But here due to negative velocity in the last seconds, the area under the curve is extended below the time axis. Hence, we have taken the difference of area under the time axis to determine displacement.