Question
Question: In the following P-V diagram of an ideal gas, AB and CD are isothermal whereas BC and DA are adiabat...
In the following P-V diagram of an ideal gas, AB and CD are isothermal whereas BC and DA are adiabatic processes. The value of VCVB is:
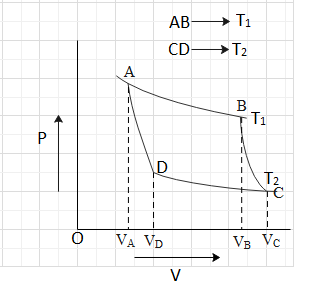
Explanation
Solution
Here in the given P-V graph there are two processes isothermal and adiabatic. When the system goes from A to B and C to D, the isothermal process is happening and when it goes from B to C and D to A, an adiabatic process is taking place. We have to find the relation between the volumes at the point A, B, C and D which can be obtained by using pressure-volume relationship for the isothermal and adiabatic process.
Formula used:
