Question
Question: In the following graph how do you determine the value of c such that \[\displaystyle \lim_{x \to c}f...
In the following graph how do you determine the value of c such that x→climf(x) exists?
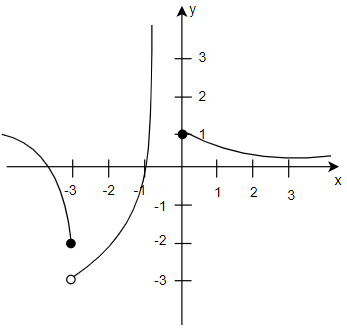
Solution
Here we have to determine the value of c such that x→climf(x) exists. We can see that in the graph the function f(x) is defined when x = -2 but the value which f(x) will approach as x gets closer to -3 from the left is different from the value as it approaches from the right. We can apply the limits by looking at the graph and find the c values.
Complete step by step solution:
Here we have to determine the value of c such that x→climf(x) exists.
We can see that in the graph the function f(x) is defined when x = -2 but the value which f(x) will approach as x gets closer to -3 from the left is different from the value as it approaches from the right.
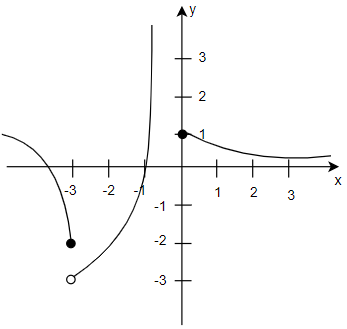
We can now analyse the graph, as x approaches -3 from left f(x) approaches (negative 2) however as x approaches -3 from the right f(x) approaches (negative 3)
We can now apply the limits, we get
