Solveeit Logo
Login

Question

Question: In the following figure, which of the following is the value of \(\csc \theta \)? ![](https://www....

In the following figure, which of the following is the value of csc⁡θ\csc \theta ?

[a] aa2+b2\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}
[b] ba2+b2\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}
[c] ba\dfrac{b}{a}
[d] a2+b2a\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{a}
[e] a2+b2b\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{b}

Explanation

Solution

Hint: Use the fact that tan⁡θ\tan \theta is the slope of the line OT. Hence find the value of tan⁡θ\tan \theta . Using the Pythagorean identity sec⁡2θ=1+tan⁡2θ{{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta , find the value of sec⁡θ\sec \theta and hence find the value of cos⁡θ\cos \theta .
Using the fact that tan⁡θ=sin⁡θcos⁡θ\tan \theta =\dfrac{\sin \theta }{\cos \theta }, find the value of sin⁡θ\sin \theta and hence find the value of csc⁡θ\csc \theta . Hence find which of the options is correct.

Complete step-by-step answer:

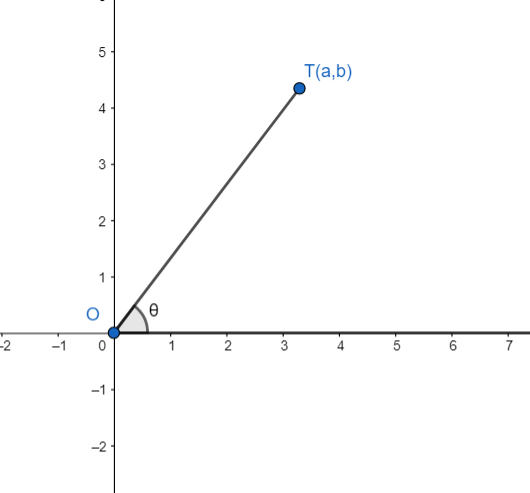
We know that the tangent of the angle made by a line with the positive direction of x-axis is the slope of the line.
Hence, we have
Slope of the line OT =tan⁡θ=\tan \theta
Now, we know that the slope of the line joining the poits A(x1,y1)A\left( {{x}_{1}},{{y}_{1}} \right)and B(x2,y2)B\left( {{x}_{2}},{{y}_{2}} \right) is given by m=y2−y1x2−x1m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}
Hence, we have
Slope of the line OT =b−0a−0=ba=\dfrac{b-0}{a-0}=\dfrac{b}{a}
Hence, we have tan⁡θ=ba\tan \theta =\dfrac{b}{a}
We know that sec⁡2θ=1+tan⁡2θ{{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta
Hence, we have
sec⁡2θ=1+b2a2=a2+b2a2{{\sec }^{2}}\theta =1+\dfrac{{{b}^{2}}}{{{a}^{2}}}=\dfrac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}}
Hence, we have
sec⁡θ=±a2+b2a\sec \theta =\pm \dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{a}
Since θ\theta lies in the first quadrant, we have sec⁡θ>0\sec \theta >0
Hence, we have
sec⁡θ=a2+b2a\sec \theta =\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{a}
We know that cos⁡θ=1sec⁡θ\cos \theta =\dfrac{1}{\sec \theta }
Substituting the value of sec⁡θ\sec \theta , we get
cos⁡θ=aa2+b2\cos \theta =\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}
Now, we know that tan⁡θ=sin⁡θcos⁡θ\tan \theta =\dfrac{\sin \theta }{\cos \theta }
Substituting the values of tan⁡θ\tan \theta and cos⁡θ\cos \theta , we get
ba=sin⁡θaa2+b2\dfrac{b}{a}=\dfrac{\sin \theta }{\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}}
Multiplying both sides by aa2+b2\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}, we get
sin⁡θ=ba2+b2\sin \theta =\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}
We know that csc⁡θ=1sin⁡θ\csc \theta =\dfrac{1}{\sin \theta }
Substituting the value of sin⁡θ\sin \theta , we get
csc⁡θ=a2+b2b\csc \theta =\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{b}
Hence option [e] is correct.

Note: Alternative solution:
Draw perpendicular TA and TB on the x-axis and the y-axis, respectively.

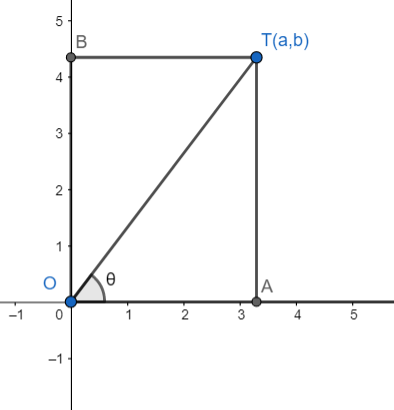
Hence, we have OA = a and OB = b.
Now, in triangle OAT, by Pythagoras theorem, we have
OT2=a2+b2⇒OT=a2+b2O{{T}^{2}}={{a}^{2}}+{{b}^{2}}\Rightarrow OT=\sqrt{{{a}^{2}}+{{b}^{2}}}
We know that cosecant of an angle is the ratio of the hypotenuse to the opposite side.
Hence, we have
csc⁡θ=OTAT=a2+b2b\csc \theta =\dfrac{OT}{AT}=\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{b}, which is the same as obtained above
Hence option [e] is correct.