Question
Question: In the following figure, two isotropic point sources \[{S_1}\]and \[{S_2}\]emit light in phase at wa...
In the following figure, two isotropic point sources S1and S2emit light in phase at wavelength λand at the same amplitude. The sources are separated by distance 2d=6.00λ. They lie on an axis that is parallel to an x axis, which runs along a viewing screen at distance D=20.0λ. The origin lies on the perpendicular bisector between the sources. The figure shows two rays reaching point P on the screen, at position xP. What multiple of λ gives the maximum phase difference?
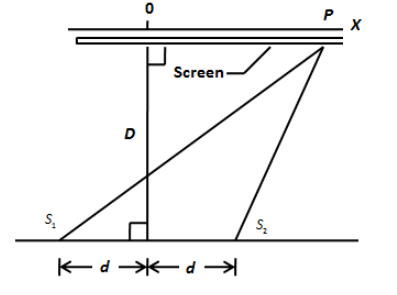
Solution
The phase difference between the rays S1P and S2P is S1P−S2P. Draw the perpendicular lines from S1 and S2 on the screen and use the geometry of the triangles formed by these lines to determine the distance of S1P and S2P. Assume d≪D.
Complete step by step answer:
We have to determine the phase difference between the rays reaching at point P. To do so, we have to redraw the above figure as,
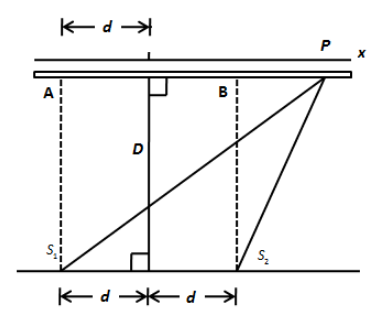
We can see the phase difference between the rays S1P and S2P is S1P−S2P. Let’s use Pythagoras theorem to determine the distance S1P. In triangle S1AP, using Pythagoras theorem, we can write,
(S1P)2=D2+(x+d)2
⇒(S1P)2=D2+x2+2xd+d2 …… (1)
In triangle S2BP, using Pythagoras theorem, we can write,
(S2P)2=D2+(x−d)2
⇒(S2P)2=D2+x2−2xd+d2 …… (2)
Subtracting equation (2) from equation (1), we get,
(S1P)2−(S2P)2=4xd
⇒(S1P−S2P)(S1P+S2P)=4xd
⇒S1P−S2P=S1P+S2P4xd
If we assume, d≪D, then we can write, S1P+S2P=2D. Therefore, the above equation becomes,
S1P−S2P=2D4xd
⇒S1P−S2P=D2xd
Substituting 2d=6.00λ, D=20.0λ and x=6.00λ, we get,
S1P−S2P=202(6)(6)
∴S1P−S2P=3.6
Therefore, the maximum phase difference is 3.6 times the wavelength.
Note: This question is clearly based on Young’s double slit experiment. Therefore, students must study YDSE to recall the concept of phase difference. In YDSE, if we draw the perpendicular line from S2 onS1P, the distance from S1 to the point where the perpendicular line meets is also the phase difference of the wave.
