Question
Question: In the following figure, O is the center of circle. Find the value of $\angle ADB$. ...
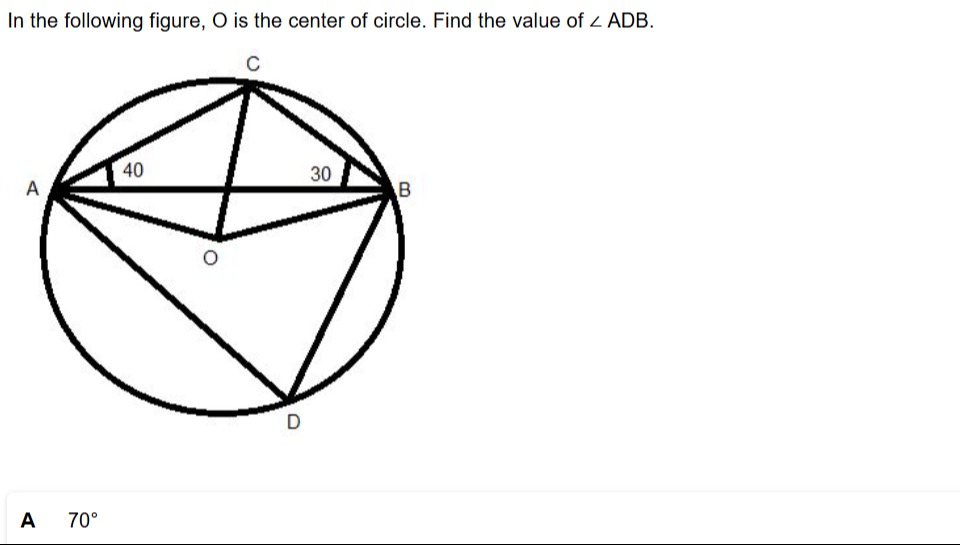
In the following figure, O is the center of circle. Find the value of ∠ADB.
70°
70°
Solution
To find the value of ∠ADB, we will use properties of circles and triangles.
1. Interpret the given angles: The angles marked 40° and 30° in the figure are ∠OAC and ∠OBC respectively. This is inferred from the placement of the angle arcs and the lines involved.
2. Use properties of isosceles triangles formed by radii:
-
In △OAC: OA and OC are radii of the same circle, so OA = OC. Therefore, △OAC is an isosceles triangle. The angles opposite to equal sides are equal, so ∠OCA=∠OAC. Given ∠OAC=40∘, thus ∠OCA=40∘.
-
In △OBC: OB and OC are radii of the same circle, so OB = OC. Therefore, △OBC is an isosceles triangle. The angles opposite to equal sides are equal, so ∠OCB=∠OBC. Given ∠OBC=30∘, thus ∠OCB=30∘.
3. Calculate ∠ACB: The angle ∠ACB is the sum of ∠OCA and ∠OCB. ∠ACB=∠OCA+∠OCB ∠ACB=40∘+30∘ ∠ACB=70∘
4. Use the property of angles in the same segment: Angles subtended by the same arc at any point on the remaining part of the circle are equal. In the given figure, arc AB subtends ∠ACB at point C and ∠ADB at point D on the circumference. Therefore, ∠ADB=∠ACB.
5. Final Value: Since ∠ACB=70∘, we have: ∠ADB=70∘
