Question

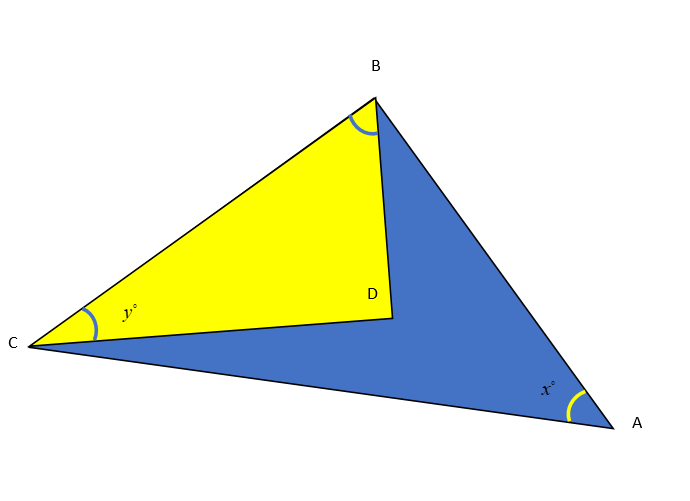
In the following figure:-
BD = 18, DC = 24, AC = 50, $\angle A = x,\angle BCD = y$ and $\angle ABC = {90^ \circ } = \angle BDC$.
Find: $5 - 3{\tan ^2}x + 3{\sec ^2}x$.

Answer 1

We will first look at the given expression whose value we are required to find. After that, we will take 3 common out of it and use the identity to get the required answer.

Step-By-Step answer:
We are given the expression: $5 - 3{\tan ^2}x + 3{\sec ^2}x$.
We can write this as:-
$\Rightarrow 5 - 3\left( {{{\tan }^2}x - {{\sec }^2}x} \right)$
Now, we have an identity which states that: $1 + {\tan ^2}x = {\sec ^2}x$
This implies that ${\tan ^2}x - {\sec ^2}x = - 1$
Putting this in the above expression, we will get:-
$\Rightarrow 5 - 3\left( {{{\tan }^2}x - {{\sec }^2}x} \right) = 5 - 3( - 1)$
Simplifying the calculations, we will then obtain:-
$\Rightarrow 5 - 3\left( {{{\tan }^2}x - {{\sec }^2}x} \right) = 8$
$\therefore 5 - 3{\tan ^2}x + 3{\sec ^2}x = 8$

Hence, the required answer is 8.

Note: The students must note that we are given some measurements of the sides and the angles in the figure but we do not actually require them to get the answer.
The students must note that they may try to use the trigonometric ratios to find the answer of the given expression but that may be not possible to be solved because we are not given value of y as well which we may use to find the value of BC. So, this is the most brief and easiest way to find the value.
The students must note that they do not require to cram the formula: $1 + {\tan ^2}x = {\sec ^2}x$.
They can use ${\sin ^2}\theta + {\cos ^2}\theta = 1$
Now divide both sides by ${\cos ^2}\theta$ to get:-
$\Rightarrow \dfrac{{{{\sin }^2}\theta }}{{{{\cos }^2}\theta }} + \dfrac{{{{\cos }^2}\theta }}{{{{\cos }^2}\theta }} = \dfrac{1}{{{{\cos }^2}\theta }}$
$\Rightarrow 1 + {\tan ^2}x = {\sec ^2}x$
Thus, we have the required formula.
Let us get to know some fun facts about the trigonometric ratios:-
Trigonometry has so many real life applications. Trigonometry is used by Engineers, Architects, Scientists and Mathematicians to calculate and evaluate so many things which are going to be extremely useful and important.
The students must also note that the students should use trigonometric ratios and formulas in the right angled triangles only. Otherwise, they will be required to drop the perpendicular from a vertex to the opposite side and then use trigonometric values in both the triangles formed by dividing the bigger triangle.
This is an extremely useful concept to have the knowledge of. You must have a brief knowledge about it.