Question
Question: In the following circuit, the resistance of a voltmeter is \( 10,000\Omega \) and that of an ammeter...
In the following circuit, the resistance of a voltmeter is 10,000Ω and that of an ammeter is 20Ω. If the reading of an ammeter is 0.1 amp. and that of voltmeter is 12 volts, then the value of R is:
(A) 122Ω
(B) 100Ω
(C) 118Ω
(D) 116Ω
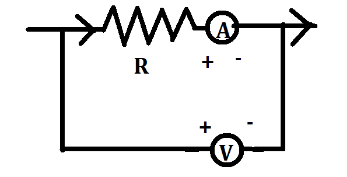
Solution
The relation between electric current and potential difference is stated by Ohm's law. The current flowing through most conductors is directly proportional with the voltage applied to it. The first to experimentally verify Ohm's law was Georg Simon Ohm, a German physicist.
Formula used:
We will use the following formula to find the answer to this simple question:
V=IR
Where
V is the voltage applied in the circuit
I is the amount of electric current applied to the circuit
R is the total resistance in the electrical circuit.
Complete step by step answer:
According to the question, the following data is provided to us
The resistance in the voltmeter is 10000Ω
The resistance in the ammeter is 20Ω
The reading of the ammeter is 0.1A
The reading of the voltmeter is 12V
Since the resistor and the resistance of the ammeter are connected in series, then the net resistance will be R+RA
Where RA is the resistance of the ammeter
So, according to the Ohm’s law, we can put these values in the expression for finding out the voltage
V=IR
V=I(R+RA)
Now we put the values of the known variables provided to us in the question
12=0.1(R+20)
⇒12=0.1R+2
Upon solving this equation, we get
⇒0.1R=10
∴R=100Ω
Hence, the correct option is (B).
Note:
The law of Ohm only holds true if the temperature provided and the other physical factors remain constant. Increasing the current in some components raises the temperature. The filament of a light bulb, in which the temperature rises when the current is increased, is an example of this. In this case, it is not possible to apply Ohm's law. Ohm's Law is violated by the light-bulb filament.
