Question
Question: In the following circuit, the current through the resistor R (\[=2\Omega \]) is I amperes. Find the ...
In the following circuit, the current through the resistor R (=2Ω) is I amperes. Find the value of I.
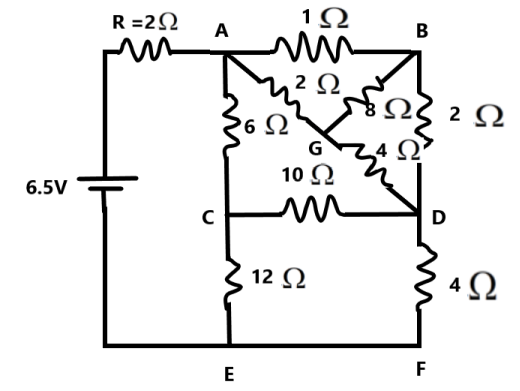
Solution
We need to find the current through a specific resistance in the given circuit. We need to find the equivalent resistance of the complete circuit and understand the current flowing through one of the resistances. We can use different methods to approach this situation.
Complete step by step answer:
We can find the current flowing through the resistor on finding the equivalent resistance of the circuit. The portion ABDFECA is in series with the resistor R. We can find the resistance of the wing ABDFECA.
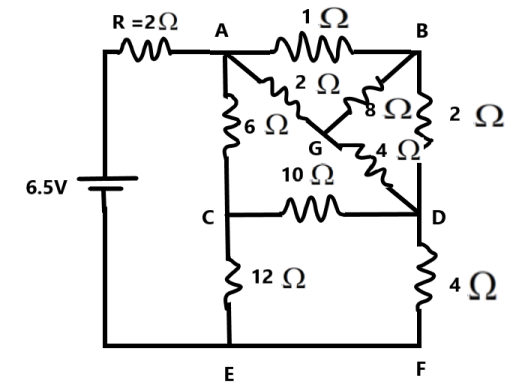
Let us consider the circuit ABDGA, we understand that the nodes B and G are in equipotential condition, therefore there is no current through the 8Ω resistor. This is in accordance with Wheatstone's bridge condition. The ratio of the resistors across BG is equal.
The resistance of the part ABDGA is given as –
