Question
Question: In the following arrangement, the system is initially at rest. The 5 kg block is now released. Assum...
In the following arrangement, the system is initially at rest. The 5 kg block is now released. Assuming the pulley and string to be massless and smooth, the acceleration of block C will be:
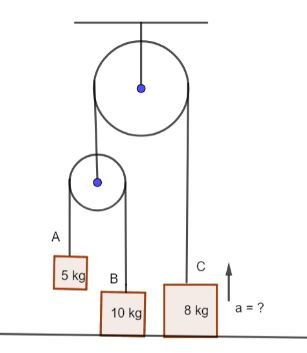
Solution
In this question, we will first draw all the forces-tension in the strings and weight of the blocks- and equate all the vertical force for a particular block to obtain two equations. Here, since block B is grounded, the acceleration will be imparted completely from block A. Hence, the acceleration of block A will be twice the acceleration of block C. On solving the two equations, we shall calculate the value of the acceleration of block C.
Complete step by step answer:
Let’s visualize the situation first.
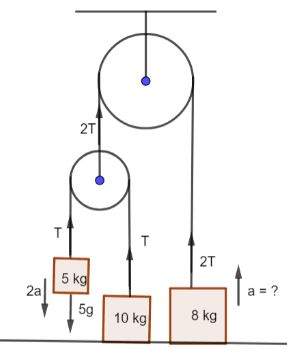
In the figure all the forces have been marked accordingly.Since nothing has been mentioned about the pulley in terms of whether they are movable or not, we shall consider them to be fixed. If we consider the string connecting the smaller pulley and the block A, the tension in the string is T.The tension in the string connecting the bigger pulley and the block C is marked 2T because the tension in the string has to remain constant.
For block A, on equating the forces to maintain the vertical equilibrium we get,
5g−T=5(2a)
⇒5g−T=10a.......(1)
For block C, on equating the forces to maintain the vertical equilibrium we get,
2T−8g=8a
⇒T−4g=4a..........(2)
Adding (1) and (2), we get
g=14a
This can be rewritten as a=14g
Taking g=10ms−2 and substituting in the above equation, we get,
a=1410ms−2
∴a=75ms−2
Hence, the acceleration of block C will be 75ms−2.
Note: Block B is grounded. Hence, we took its acceleration to zero. Also, the pulleys were fixed. Had they been movable, they would have also experienced an acceleration which must be accounted for while calculating the acceleration of block C. Also, the tension remained constant throughout the string because it was given that the string was smooth.
