Question
Question: In the figures shown, a massless spring of stiffness \(k=100\;Nm^{-1}\) and natural length \(l_0\) i...
In the figures shown, a massless spring of stiffness k=100Nm−1 and natural length l0 is rigidly attached to a block of mass m=20kg and is in vertical position. A wooden ball of the same mass is released from rest to fall under gravity. Having fallen a heighth the ball strikes the spring and gets stuck up in the spring at the top. What should be the minimum value ofh (in m) so that the lower block will just lose contact with the ground later on? Neglect any loss of energy.
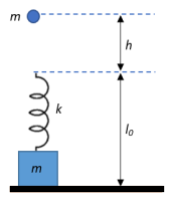
Solution
Begin by deducing the forces that influence our system, i.e., gravitational force and spring force. Determine the work done by the gravitational force and the spring force. Recall that the work done by the spring force will be the difference in the potential energy possessed by the spring at initial position and final displacement, and that of gravitational force will be by virtue of the gravitational potential energy possessed by the ball at different heights. To this end, use the work-energy theorem and arrive at an equation for the minimum height that the ball must be released from and plug in the given values to obtain the appropriate result.
Formula Used:
Work-energy theorem: Wnet=ΔKE
Wgravitational=mgh
Wspring=21kx2
Complete step-by-step solution:
We are given that a wooden ball falls through a heighth and strikes a spring whose other end is connected to a block of massm. The ball gets struck in the spring, pushing down on the spring, making the spring recoil and push itself and the ball with it upwards through a displacement of, sayx, as shown in the figure.
The weight of the block acts downwards as gravitational force :
Fg=mg
From Hooke’s law, the spring force as a result of the extension of the spring throughx when the ball gets stuck and subsequently gets recoiled by the spring will be:
Fs=kx, where k is the spring constant indicating the stiffness of the spring.
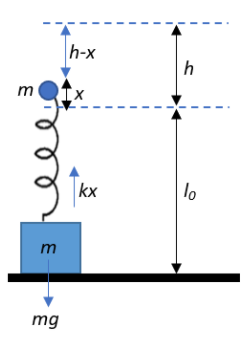
Now, for the block to just lose contact with the ground, the spring force acting on the block must be able to pull the block up and be at least equal to the weight of the block, i.e.,
Fs=Fg⇒kx=mg⇒x=kmg
Now, the work done by the spring force will be the difference in the potential energy possessed by the spring at initial displacement (x1=0) and final displacement (x2=x), i.e.,
Ws=21k(x12−x22)=21k(0−x2)=−21kx2
But we have x=kmg
⇒Ws=−21k(kmg)2
And the work done by the gravitational force will be the difference in the potential energy possessed by the ball at its initial position (h) and final position (x), i.e.,
Wg=mgh–mgx=mg(h−x)
But we have x=kmg
⇒Wg=mg(h−kmg)
From the work energy theorem which states that the net work done by the forces on an object equals the change in its kinetic energy, we have:
Wg+Ws=ΔKE
Since the ball is released from rest, its initial velocity is zero, which means that its initial kinetic energy is zero. Then, the ball gets stuck in the spring, so the final velocity of the ball is zero, implying that the final kinetic energy of the ball is zero. Therefore, ΔKE=0.
⇒Wg+Ws=0
⇒mg(h−kmg)−21k(kmg)2=0
⇒mg(h−kmg)=21k(kmg)2
⇒(h−kmg)=21(kmg)
⇒h=2kmg+kmg=2k3mg
Given that m=20kg, k=100Nm−1 and g=10ms−2:
h=2k3mg=2×1003×20×10=3m
Therefore, the ball must be dropped from a height of at least 3m so that the lower block may just lose contact with the ground later on.
Note: Always remember to account for all forces while considering the work done by the forces acting in the system. All forces here, mean only those forces that contribute to changing the kinetic energy of a body, which is why we considered the gravitational and spring force in our case.
Also, when a body is released from a height under the influence of gravity, it possesses potential energy which gets translated into kinetic energy facilitating the motion of the body. The work done by the gravitational potential is equivalent to this change in kinetic energy of the body in accordance with the work-energy theorem, but it is only in this case that we assume that all the mechanical energy is converted to heat energy and not straight up kinetic energy, like we did in the above problem. Therefore, remember to tweak the work-energy theorem to suit the context of the problem statement.
