Question

In the figure which voltmeter reads zero, when $\omega$ is equal to the resonant frequency of the series LCR circuit?

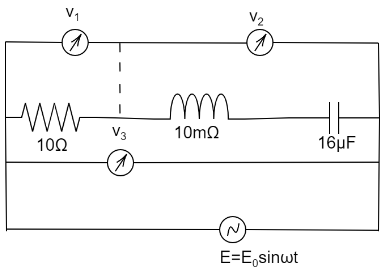
A). ${V_1}$
B). ${V_2}$
C). ${V_3}$

Answer 1

An LCR circuit has three major components: resistor, inductor, capacitor.
These components can be connected in either a series or a parallel configuration.
Impedance is lowest at resonance in the LCR series. As a result, ${Z_{\min }} = R$ . $\omega$ is the angular frequency.

Complete Step By Step Answer:
A voltmeter will read zero when the points being measured are of the same potential.
Let the voltage across the inductor be ${V_L}$ and voltage across the capacitor be ${V_C}$ .
Voltage across the resistor is given by ${V_1} = IR$ , where I is the current and R is the resistance.
Voltage across inductor and capacitor is given by ${V_2} = {V_L} - {V_C}$
Therefore voltage across ${V_3}$ is given by ${V_3}^2 = {V_1}^2 + {({V_L} - {V_C})^2}$
Only the presence of resistor affect the voltage through the voltmeter ${V_1}$ , the inductor and the capacitor affect the voltage through the voltmeter ${V_2}$ , all three components affects the voltage through the voltmeter ${V_3}$
Since the resonance voltage across the inductor and capacitor will be the same.
That is ${V_L} = {V_C}$
$\Rightarrow {V_L} - {V_C} = 0$
$\Rightarrow$ voltage across the voltmeter ${V_2}$ will be zero.
The correct answer is option B, ${V_2}$ .

Note:
The frequency at which the impedance of the LCR circuit becomes minimal or the current in the circuit becomes maximal is known as the resonance frequency.
Resonant frequency ${\omega _r} = = \dfrac{1}{{\sqrt {LC} }}$
LCR circuits have a significant amount of resonance. Energy can be stored in LCR circuits in two ways: as an electric field in a capacitor when it is charged, or as a magnetic field in an inductor when current runs through it.