Question

In the figure, what is the potential difference between the points A and B and between B and C respectively in steady state.

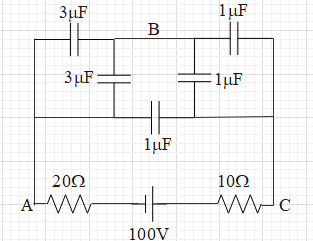
A. ${{V}_{AB}}={{V}_{BC}}=100V$
B. ${{V}_{AB}}=75V,{{V}_{BC}}=25V$
C. ${{V}_{AB}}=25V,{{V}_{BC}}=75V$
D. ${{V}_{AB}}={{V}_{BC}}=50V$

Answer 1

Hint : The current in the circuit is zero, as it is in steady state. Further analyse the circuit and calculate its equivalent capacitance to find the total charge in the circuit. Then use the formula for the potential difference across a capacitor and find the required voltages.
${{C}_{eq}}={{C}_{1}}+{{C}_{2}}$ , when two capacitors are in parallel connection.
${{C}_{eq}}=\dfrac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}}$ , when two capacitors are in series connection.
$V=\dfrac{Q}{C}$ , where V is the voltage across a capacitance C with charge Q.

Complete Step By Step Answer:
It is said that the circuit is in steady state. This means that the capacitors are fully charged and there is no current passing in the circuit.
Therefore, we shall short the two resistances, by replacing them with connecting wires. Then we can see that the two capacitors of $3\mu F$ each, are in parallel connection. Therefore, the equivalent capacitance of these two is equal to ${{C}_{eq}}=3\mu +3\mu =6\mu F$ .
Similarly, the two capacitors of $1\mu F$ are also in parallel connection. The equivalent capacitance of these two is equal to ${{C}_{eq}}=1\mu +1\mu =2\mu F$ .
With this analysis, we can reconstruct the same circuit as shown below.

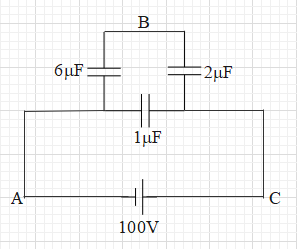
Now, we can see that the capacitors of $6\mu F$ and $2\mu F$ are in series connection and the capacitor of $1\mu F$ is in parallel connection with these two.
Therefore, the equivalent capacitance of $6\mu F$ and $2\mu F$ is equal to ${{C}_{eq}}=\dfrac{(6\mu )(2\mu )}{6\mu +2\mu }=\dfrac{3\mu }{2}F$ .
This $\dfrac{3\mu }{2}F$ capacitor is in parallel connection with the $1\mu F$ capacitor.
Therefore, the equivalent capacitance of the whole circuit is ${{C}_{eq}}=1\mu +\dfrac{3\mu }{2}=\dfrac{5\mu }{2}F$
The potential difference across the whole combination is ${{V}_{AC}}=100V$ .
Therefore, the positive charge stored in the circuit is $Q=\left( \dfrac{5}{2}\mu \right)(100)=250\mu C$
The potential difference across the $1\mu F$ capacitor is equal to ${{V}_{AC}}=100V$ .
Therefore, the charge on these capacitors is equal to ${{Q}_{1}}=(1\mu )(100)=100\mu C$ .
Therefore, the charge on the capacitors of $6\mu F$ and $2\mu F$ is ${{Q}_{2}}=Q-{{Q}_{1}}=150\mu C$ .
Now, the potential difference on the capacitor $6\mu F$ is ${{V}_{AB}}=\dfrac{{{Q}_{2}}}{6\mu F}$ .
Then,
$\Rightarrow {{V}_{AB}}=\dfrac{150\mu C}{6\mu F}=25V$
The potential difference on the capacitor $2\mu F$ is ${{V}_{BC}}=\dfrac{{{Q}_{2}}}{2\mu F}$ .
Then,
$\Rightarrow {{V}_{BC}}=\dfrac{150\mu C}{2\mu F}=75V$
Hence, the correct option is C.

Note :
You can cross check your answer by the knowledge that ${{V}_{AB}}+{{V}_{BC}}={{V}_{AC}}=100V$ .
Note that when the capacitors are in series connection, the charge on each of the capacitors is equal.
And when the capacitors are in parallel connection, the potential difference across each capacitor is equal.