Solveeit Logo
Login

Question

Question: In the figure \(\vartriangle ABC\) and \(\vartriangle ABD\) are two triangles on the same base AB. I...

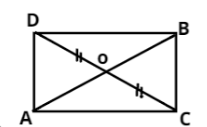
In the figure △ABC\vartriangle ABC and △ABD\vartriangle ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O. Show that area(△ABC)=area(△ABD)area\left( {\vartriangle ABC} \right) = area\left( {\vartriangle ABD} \right)

Explanation

Solution

Hint: Here we apply the area of triangle theorem where median divides the triangle in two equal areas.

Complete step-by-step answer:
In △ABC\vartriangle ABC
AO is the median, (CD is bisected by AB at O)
As you know, the median divides the triangle in two equal areas.
So,area(△AOC)=area(△AOD)area\left( {\vartriangle AOC} \right) = area\left( {\vartriangle AOD} \right) …… (1)
Also, in △BCD\vartriangle BCD
BO is the median, (CD is bisected by AB at O)
So, area(△BOC)=area(△BOD)area\left( {\vartriangle BOC} \right) = area\left( {\vartriangle BOD} \right) …… (2)
Adding (1) and (2) equations
area(△AOC)+area(△BOC)=area(△AOD)=area(△BOD)area\left( {\vartriangle AOC} \right) + area\left( {\vartriangle BOC} \right) = area\left( {\vartriangle AOD} \right) = area\left( {\vartriangle BOD} \right)
⇒area(△ABC)=area(△ABD)\Rightarrow area\left( {\vartriangle ABC} \right) = area\left( {\vartriangle ABD} \right)

Note: Whenever you come to this type of problem you have to know about median divide the triangle in two equal areas. So for easy solving you know about theorems regarding the area of a triangle.