Question

In the figure there is a uniform conducting structure in which each small square has side a = 1 m. The structure is kept in uniform magnetic field B = 2 Tesla along BC.. Current of 2 amperes enters the structure at A and leaves at C. Find the correct option(s).

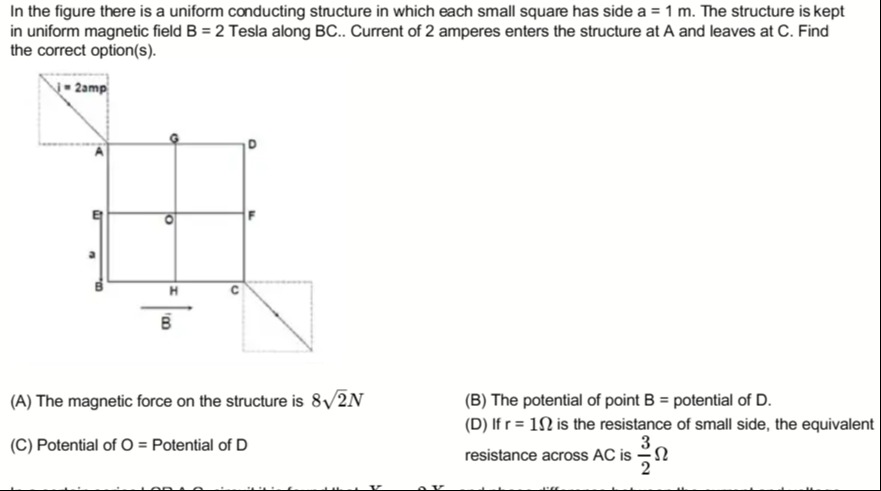
• A. The magnetic force on the structure is $8\sqrt{2}N$
• B. The potential of point B = potential of D.
• C. Potential of O = Potential of D
• D. If r = $1\Omega$ is the resistance of small side, the equivalent resistance across AC is $\frac{3}{2}\Omega$

Answer 1

Answer: (B), (C), (D)

B, C, D

Answer 2

The problem involves analyzing a uniform conducting structure in a magnetic field with current flowing through it. We need to evaluate four options related to magnetic force, potentials, and equivalent resistance.

Given:

• Side of each small square, a = 1 m.
• Magnetic field, B = 2 Tesla along BC.
• Current, I = 2 A enters at A and leaves at C.
• Resistance of each small side, r = 1 Ω.

Let's set up a coordinate system with B at the origin (0,0). Then C is at (2a, 0), E is at (0, a), A is at (0, 2a), H is at (a, 0), O is at (a, a), F is at (2a, a), G is at (a, 2a), D is at (2a, 2a). Since a = 1 m: A = (0, 2), C = (2, 0) B = (0, 0), D = (2, 2) E = (0, 1), F = (2, 1), G = (1, 2), H = (1, 0), O = (1, 1)

Option (A): The magnetic force on the structure is $8\sqrt{2}N$.

For a current-carrying conductor in a uniform magnetic field, the net magnetic force is given by $\vec{F} = I (\vec{L} \times \vec{B})$, where $\vec{L}$ is the displacement vector from the point where current enters to the point where it leaves. Here, current enters at A and leaves at C. The displacement vector $\vec{L} = \vec{AC} = C - A = (2-0)\hat{i} + (0-2)\hat{j} = 2\hat{i} - 2\hat{j}$ m. The magnetic field $\vec{B}$ is along BC. Since B=(0,0) and C=(2,0), BC is along the positive x-axis. So, $\vec{B} = B\hat{i} = 2\hat{i}$ Tesla. The current $I = 2$ A.

Now, calculate the force: $\vec{F} = I (\vec{L} \times \vec{B})$ $\vec{F} = 2 \text{ A} \times ((2\hat{i} - 2\hat{j}) \text{ m} \times (2\hat{i}) \text{ T})$ $\vec{F} = 2 \times ( (2 \times 2)(\hat{i} \times \hat{i}) - (2 \times 2)(\hat{j} \times \hat{i}) )$ We know $\hat{i} \times \hat{i} = 0$ and $\hat{j} \times \hat{i} = -\hat{k}$. $\vec{F} = 2 \times (0 - 4(-\hat{k}))$ $\vec{F} = 2 \times (4\hat{k})$ $\vec{F} = 8\hat{k}$ N. The magnitude of the force is $|\vec{F}| = 8$ N. Therefore, option (A) is incorrect.

Option (B): The potential of point B = potential of D.

The structure is symmetric about the diagonal AC. Current enters at A and leaves at C. Points that are images of each other across the diagonal AC (the line connecting the input and output terminals) will be at the same potential. Points B and D are symmetric with respect to the diagonal AC. Therefore, $V_B = V_D$. This can also be shown by current distribution: Let $I_{AE}$ be the current from A to E, and $I_{AG}$ be the current from A to G. By symmetry, $I_{AE} = I_{AG} = I/2$. Let $I_{EB}$ be current from E to B, and $I_{EO}$ from E to O. Let $I_{GD}$ be current from G to D, and $I_{GO}$ from G to O. Due to symmetry ($AE \leftrightarrow AG$, $EB \leftrightarrow GD$, $EO \leftrightarrow GO$), $I_{EB} = I_{GD}$ and $I_{EO} = I_{GO}$. Now consider potentials: $V_A - V_E = I_{AE}r$ $V_A - V_G = I_{AG}r$ Since $I_{AE} = I_{AG}$, we have $V_E = V_G$. Then, $V_E - V_B = I_{EB}r$ and $V_G - V_D = I_{GD}r$. Since $V_E = V_G$ and $I_{EB} = I_{GD}$, it implies $V_B = V_D$. Therefore, option (B) is correct.

Option (C): Potential of O = Potential of D.

From the analysis in (B), we know $V_B = V_D$. So, this option is equivalent to checking if $V_O = V_B$. Let's find the current distribution more precisely. By symmetry, the circuit can be folded along the diagonal AC. The points E and G are equipotential ($V_E = V_G$). The points B and D are equipotential ($V_B = V_D$). The points H and F are equipotential ($V_H = V_F$). Let $I_1$ be current in AE and AG. So $I_1 = I/2 = 2/2 = 1$ A. Let $I_2$ be current in EB and GD. Let $I_3$ be current in EO and GO. At node E (or G): $I_1 = I_2 + I_3$. Let $I_4$ be current in BH and DF. Let $I_5$ be current in OH and OF. At node B (or D): $I_2 = I_4$. (Since B only connects to H). At node O: $I_3 + I_3 = I_5 + I_5 \implies I_5 = I_3$. (Currents from E and G enter O, and then current leaves O via H and F). At node H (or F): $I_4 + I_5 = I_{HC}$ (or $I_{FC}$). So, $I_2 + I_3 = I_{HC}$. Total current leaving C is $I_{HC} + I_{FC} = 2(I_2+I_3) = I$. This is consistent with $I_1 = I/2 = I_2+I_3$.

Now let's find the potentials relative to $V_C = 0$. $V_H = I_{HC} r = (I_2+I_3)r$. $V_B = V_H + I_{BH}r = (I_2+I_3)r + I_2 r = (2I_2+I_3)r$. $V_O = V_H + I_{OH}r = (I_2+I_3)r + I_3 r = (I_2+2I_3)r$. For $V_O = V_D$ (or $V_O = V_B$), we need $(I_2+2I_3)r = (2I_2+I_3)r$, which implies $I_2 = I_3$. If $I_2 = I_3$, then $V_E - V_B = I_2 r$ and $V_E - V_O = I_3 r$. This would mean $V_B = V_O$. Let's see if $I_2 = I_3$. The current $I_1$ splits into $I_2$ and $I_3$ at node E. Path E-B-H-C has resistance $3r$. Path E-O-H-C has resistance $2r$. Since $R_{EB} = r$ and $R_{EO} = r$, the currents $I_2$ and $I_3$ depend on the resistance of the rest of the path. The part of the circuit starting from E can be seen as: E to B (r) then B to H (r) then H to C (r). Total $3r$. E to O (r) then O to H (r) then H to C (r). Total $3r$. E to O (r) then O to F (r) then F to C (r). Total $3r$. This is not a simple parallel combination.

Let's use the equivalent resistance calculation (from Option D). The equivalent resistance of the network across AC is $R_{eq} = \frac{3}{2}r$. With $r=1\Omega$, $R_{eq} = 1.5\Omega$. Total current $I=2A$. $V_A - V_C = I \cdot R_{eq} = 2 \times 1.5 = 3$ V. Let $V_C = 0$, so $V_A = 3$ V.

Let's find potentials using current values. Let $I_{AE} = I_{AG} = I_1 = 1$ A. Let $I_{EB} = I_2$, $I_{EO} = I_3$. So $I_2+I_3 = 1$. Let $I_{BH} = I_4$, $I_{OH} = I_5$. At B: $I_2 = I_4$. At O: $I_3 + I_3 = I_5 + I_5 \implies I_5 = I_3$. At H: $I_4 + I_5 = I_{HC}$. So $I_2+I_3 = I_{HC} = 1$ A. $V_C=0$. $V_H = I_{HC}r = (1)(1) = 1$ V. $V_B = V_H + I_4 r = 1 + I_2(1) = 1+I_2$. $V_O = V_H + I_5 r = 1 + I_3(1) = 1+I_3$. $V_E = V_B + I_2 r = (1+I_2) + I_2(1) = 1+2I_2$. Also $V_E = V_O + I_3 r = (1+I_3) + I_3(1) = 1+2I_3$. From $1+2I_2 = 1+2I_3$, we get $I_2 = I_3$. Since $I_2+I_3 = 1$, we have $2I_2 = 1 \implies I_2 = 0.5$ A. And $I_3 = 0.5$ A.

Now check potentials: $V_H = 1$ V. $V_B = 1 + I_2 = 1 + 0.5 = 1.5$ V. $V_D = V_B = 1.5$ V. (Confirmed B is correct) $V_O = 1 + I_3 = 1 + 0.5 = 1.5$ V. So, $V_O = V_D = 1.5$ V. Therefore, option (C) is correct.

Option (D): If r = $1\Omega$ is the resistance of small side, the equivalent resistance across AC is $\frac{3}{2}\Omega$.

We can use the current distribution found above. $V_A = V_E + I_1 r = (1+2I_2) + I_1(1) = (1+2(0.5)) + 1 = (1+1)+1 = 3$ V. The equivalent resistance $R_{eq} = V_A / I = 3 \text{ V} / 2 \text{ A} = 1.5 \Omega = \frac{3}{2}\Omega$. Therefore, option (D) is correct.

Summary of correct options: Options (B), (C), and (D) are correct.

Final Answer Check: A: Force is 8N, not $8\sqrt{2}N$. (Incorrect) B: $V_B = V_D = 1.5V$. (Correct) C: $V_O = 1.5V$. Since $V_D = 1.5V$, $V_O = V_D$. (Correct) D: $R_{eq} = 1.5\Omega = \frac{3}{2}\Omega$. (Correct)

The final answer is $\boxed{\text{B, C, D}}$.

Explanation of the solution:

1. Magnetic Force (A): The magnetic force on the entire structure in a uniform magnetic field is calculated using the effective length vector from the entry point (A) to the exit point (C). $\vec{L} = \vec{AC} = (2a\hat{i} - 2a\hat{j})$. Given $a=1$m, $\vec{L} = (2\hat{i} - 2\hat{j})$m. The magnetic field is $\vec{B} = 2\hat{i}$ T. The force $\vec{F} = I(\vec{L} \times \vec{B}) = 2((2\hat{i} - 2\hat{j}) \times 2\hat{i}) = 2(4(\hat{i} \times \hat{i}) - 4(\hat{j} \times \hat{i})) = 2(0 - 4(-\hat{k})) = 8\hat{k}$ N. The magnitude is 8 N. So (A) is incorrect.
2. Potential Symmetry (B, C): Due to the geometric symmetry of the structure and the current entry/exit points (A and C) being diagonally opposite corners, the network is symmetric about the diagonal AC. Points that are mirror images across the diagonal AC have the same potential. Points B and D are symmetric about AC, hence $V_B = V_D$. This confirms (B). For (C), we determined the current distribution using symmetry. Let $I_{AE}=I_{AG}=I_1$, $I_{EB}=I_{GD}=I_2$, $I_{EO}=I_{GO}=I_3$. Also, $I_1 = I_2+I_3$. By applying Kirchhoff's voltage law and current law, or by observing potential drops, we found that $I_2=I_3=0.5$ A (since $I_1=1$ A). With $V_C=0$ and $r=1\Omega$: $V_H = I_{HC}r = (I_2+I_3)r = (0.5+0.5) \times 1 = 1$ V. $V_B = V_H + I_{BH}r = V_H + I_2 r = 1 + 0.5 \times 1 = 1.5$ V. $V_D = V_B = 1.5$ V. $V_O = V_H + I_{OH}r = V_H + I_3 r = 1 + 0.5 \times 1 = 1.5$ V. Since $V_O = 1.5$ V and $V_D = 1.5$ V, $V_O = V_D$. This confirms (C).
3. Equivalent Resistance (D): The potential at A is $V_A = V_E + I_{AE}r = (V_O + I_{EO}r) + I_1 r = (1.5 + 0.5 \times 1) + 1 \times 1 = 2+1 = 3$ V. The total current $I = 2$ A. The equivalent resistance $R_{eq} = V_A/I = 3 \text{ V} / 2 \text{ A} = 1.5 \Omega = \frac{3}{2}\Omega$. This confirms (D).

The final answer is $\boxed{\text{B, C, D}}$.