Question
Question: In the figure, there are two sliders and they can slide on two frictionless parallel wires in unifor...
In the figure, there are two sliders and they can slide on two frictionless parallel wires in uniform magnetic field B, which is present everywhere. The mass of each slider is m, resistance R and initially, these are at rest. Now, if one slider is given a velocity v0=16ms−1 , what will be the velocity (inms−1) of other sliders after a long time? (Neglect the self-induction)
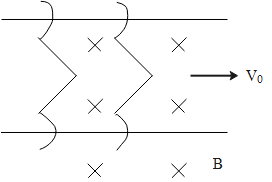
Solution
When a conductor experiences any change in the externally applied field a small force (emf) is developed in the conductor. This force will try to increase or decrease the speed of the moving conductor according to the direction of the induced force. When more than one conductor is continuously moving the mutual momentum of the conductor always remains the same (constant).
Complete step by step solution:
Initially v=0
The initial velocity of one slider v0=16m/s
Consider the following circuit mentioned in the question at t=0 due to motion of wire a current is induced in the loop due to which current a magnetic force will generate act on the wire as shown in the following diagram,
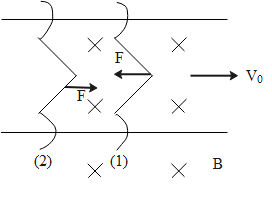
Due to this current and force on the wire speed of wire-2 increases and wire-1 decreases. After a long time when both the wires have no relative velocity between them, the flux charge between them becomes zero, and the induced current becomes zero.
So, according to the law of conservation of linear momentum, the net initial momentum should be equal to the net final momentum of the body (conductor). By applying the law of conservation of linear momentum in the situation given in the question,
pi=pf
mv0=mv+mvv=2v0
Thus the velocity of wire (2) will be,
v=216⇒v=8m/s
Thus, 8m/s is the required answer to the question.
Note: When a current-carrying conductor experiences a changing flux an emf is induced in the circuit. This is known as induction. Broadly there are two kinds of induction one is self-induction and another is mutual induction. In self-inductance, only one conductor is involved in mutual inductance two conductors come into play.
