Question
Question: In the figure there are n identical spheres of mass m suspended with wires of equal length. The sphe...
In the figure there are n identical spheres of mass m suspended with wires of equal length. The spheres are almost in contact with each other. Sphere 1 is pulled aside and released . If sphere 1 strikes sphere 2 with velocity u. find an expression for velocity vn of the nth sphere immediately after being struck by the one adjacent to it. The coefficient of restitution for all the impacts is e.
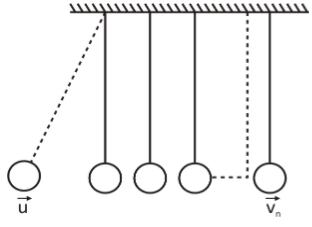
Solution
you need to find velocity of sphere after first collision and then find out the relationship between the velocities before and after collision. Once you know the relation you can find the velocity for nth collision.
Complete step by step answer:
let velocities after first collision be v1 and v2
wherev1is velocity of the first particle and v2 is velocity of the second particle.
applying momentum conservation we have
initialmomentum=finalmomentum⇒mu=mv1+mv2
And e=uv2−v1⇒eu=v2−v1
Solving both the equations
eu=v2−(u−v2)⇒v2=2(e+1)u
As we can see velocity changes by a factor of 2e+1after each collision
So after nth collision velocity will change by a factor of 2n(e+1)n
Therefore , vn=2n(e+1)nu
Note:
Although pendulums are colliding but they are colliding in its lowest position(horizontally) so we can treat it as a spheres colliding in plane ground. And if there are multiple collisions on a single sphere we should neglect it unless asked.
