Question

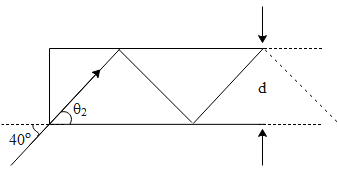
In the figure the optical fiber is l=2m and has a diameter of $d=20\mu m$.If the ray of light is incident on one end of fiber at angle ${{\theta }_{1}}={{40}^{o}}$, the number of reflection it makes before emerging from the other end is close to: ( refractive index of fiber is 1.31 and $Sin{{40}^{\circ }}=0.64$)

a)55000
b)57000
c)66000
d)45000

Answer 1

In the above given figure of the optical fiber we first have to determine the ${{\theta }_{2}}$ Using the Snell’s law. Once we know this angle across what length of the tube the first reflection takes place. Further we can infer that ‘n’ the successive reflections will take place across the total length of the fiber such that each individual reflection will take place across the length through which the first reflection was observed., Therefore we can imply that the n reflections times the length of o first reflection across the optical fiber will be equal to the total length of the fiber. Using this we will determine the total reflections.
Formula used:
$\eta =\dfrac{Sin(i)}{Sin(r)}$

Complete answer:
Let us say a ray of light is incident at an angle i on a surface having refractive index $\eta$with respect to air. If r is the angle of refraction than using Snell’s law, the required relation between the above parameters is given by,
$\eta =\dfrac{Sin(i)}{Sin(r)}$
In the above figure we can see that a ray of light is incident on the optical fiber at an angle 40 degrees. The angle ${{\theta }_{2}}$ i.e. angle of refraction from Snell’s law is equal to,
$\begin{aligned} & \eta =\dfrac{Sin(i)}{Sin(r)}\text{, }\eta =1.31\text{ and }Sin{{40}^{\circ }}=0.64 \\\ & \Rightarrow 1.31=\dfrac{Sin(40)}{Sin({{\theta }_{2}})}=\dfrac{0.64}{Sin(r)} \\\ & \Rightarrow Sin({{\theta }_{2}})=\dfrac{0.64}{1.31} \\\ & \Rightarrow {{\theta }_{2}}\simeq {{30}^{\text{o}}} \\\ \end{aligned}$

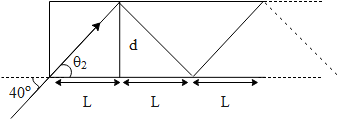
In the above figure if we observe, we can see that across length L we can imply a single reflection takes place. Observing the geometry from the above figure we can say,
$\begin{aligned} & \tan {{\theta }_{2}}=\dfrac{d}{L} \\\ & \Rightarrow L=\dfrac{d}{\tan {{\theta }_{2}}}\text{, }{{\theta }_{2}}={{30}^{\circ }}and\text{ }d=20\mu m=20\times {{10}^{-6}}m \\\ & \Rightarrow L=\dfrac{20\times {{10}^{-6}}}{\tan {{30}^{\circ }}}\text{, }\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}} \\\ & \Rightarrow L=20\sqrt{3}\times {{10}^{-6}}m \\\ \end{aligned}$
Now if we multiply n where n is the total number of reflections to L, it will be equal to the total length (D)of the optical fiber. Mathematically this can be represented as,
$\begin{aligned} & nL=D\text{, }D=2m\text{ }and\text{ }L=20\sqrt{3}\times {{10}^{-6}}m \\\ & \Rightarrow n(20\sqrt{3}\times {{10}^{-6}}m)=2m \\\ & \Rightarrow n=\dfrac{2}{20\sqrt{3}\times {{10}^{-6}}}=\dfrac{{{10}^{6}}}{10\sqrt{3}}=0.57\times {{10}^{5}}\simeq 57000 \\\ \end{aligned}$

So, the correct answer is “Option B”.

Note:
The trigonometric function i.e. tan of an angle is nothing but the ratio of the opposite side to the adjacent side of the right angled triangle. To understand the above solution better just extend the above optical fiber. You will observe that for a particular length L there exists only one reflection. Basically the value obtained in the above solution is approximate, as towards the end maybe we have considered the reflection to take place towards the end but in reality it will not.