Question

In the figure the emf of the cell is 2V and internal resistance is negligible. The resistance of the voltmeter is 80 ohms. The reading on the voltmeter will be

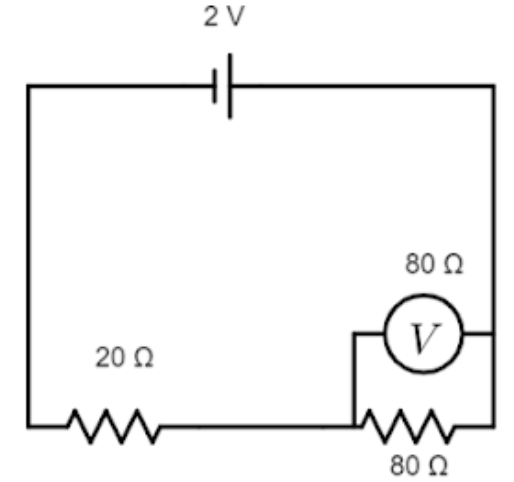
A. 2 volt
B. 1.33 volt
C. 1.60 volt
D. 0.80 volt

Answer 1

As the voltmeter has a resistance comparable to the component it has been applied across, we will not ignore the resistance on the voltmeter and will consider it a part of the circuit and solve for the potential difference accordingly.

Formula used:
Sum of resistance in series
$R={{R}_{1}}+{{R}_{2}}$
Sum of resistances in parallel
$\dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$
Ohm’s Law
$V=IR$

Complete step-by-step solution:
As the resistance of the component the voltmeter has been applied across is comparable to the resistance of the voltmeter, we will consider the resistance of the Voltmeter and can redraw the circuit as such

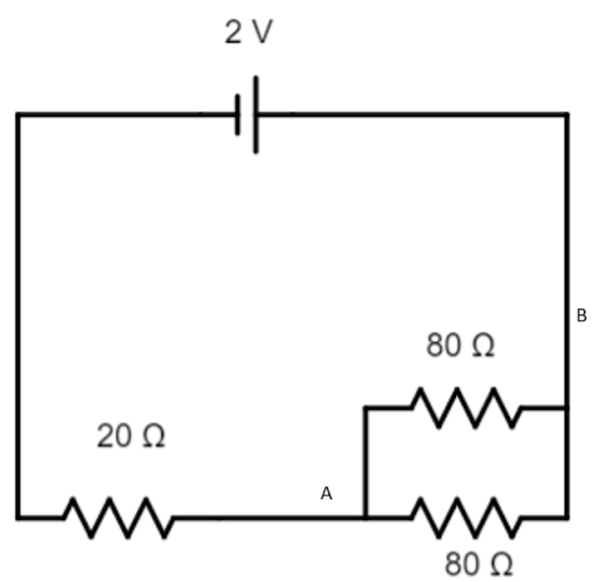
And now we will have to find the potential difference between points A and B. First, we will find the resultant resistance between the points. Using the formula for Sum of resistances in the parallel arrangement we get
$\begin{aligned} & \Rightarrow\dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}=\dfrac{1}{80}+\dfrac{1}{80}=\dfrac{2}{80} \\\ & \Rightarrow R=40\Omega \\\ \end{aligned}$
The total resistance for the circuit will be the sum of this equivalent resistance and the remaining resistance.
Total resistance $=40+20=60\Omega$
Using ohm’s law, we get the current through the circuit as
$V=IR\Rightarrow I=\dfrac{V}{R}=\dfrac{2}{60}=\dfrac{1}{30}A$
Now, due to this current, the potential difference on the equivalent resistance due to the resistances in the parallel arrangement is
$V=IR=\dfrac{1}{30}\times 40=\dfrac{4}{3}=1.33V$.
This is the potential difference between points A and B and this will be the potential difference across the voltmeter and be displayed on the voltmeter. Hence, the correct option is B, i.e. 1.33 volt.

Note: The resistances in the voltmeter must be very high so that they don’t interfere with the circuit. The voltmeter used in the given problem must not have been designed to be used in such a circuit and must have been designed to be used in systems where very low resistances are used.