Question
Question: In the figure, the cross-sectional area of the smaller tube is \[a\] and that of the larger tube is ...
In the figure, the cross-sectional area of the smaller tube is a and that of the larger tube is 2a. A block of mass m is kept in the smaller tube having the same base area a, as that of the tube. The difference between water levels of the two tubes is
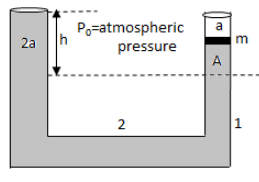
A. ρgP0+aρm
B. ρgP0+2aρm
C. aρm
D. 2aρm
Solution
Use Pascal's law. Determine the pressure of the liquid in the larger tube at depth h from the surface of the larger tube and the pressure in the liquid at the same horizontal level at depth h in the smaller tube. Equate the values of both pressures and determine the difference between the water levels of the tube which is the required answer.
Formulae used:
The pressure-depth relation is given by
P=P0+ρgh …… (1)
Here, P0 is the atmospheric pressure, ρ is the density of liquid, g is acceleration due to gravity and P is the pressure of the liquid at depth h.
The pressure P is given by
P=AF …… (2)
Here, F is the force and A is the area on which force is applied.
Complete step by step answer:
We can redraw the given diagram as follows:
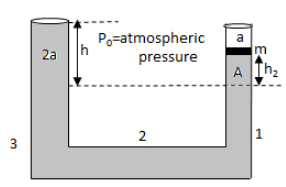
In the above diagram, h1 is the height of the liquid for the horizontal level at which the pressure in both the tubes are equal. We know that according to Pascal’s law of pressure, the pressure of the liquid at the same horizontal level is the same. The pressure PL of the liquid at depth h from the surface of the tube is given by equation (1).
PL=P0+ρgh
The pressure PS of the liquid at depth h1 from the surface of the tube is the sum of the pressure Ph1 given by equation (1) and the pressure Pb due to weight of the block.
PS=Ph1+Pb …… (3)
Rewrite equation (1) for the pressure Ph1 of liquid at depth h1 from the surface of the smaller tube.
Ph1=P0+ρgh1
Rewrite equation (2) for pressure Pb due to weight of the block.
Pb=amg
Substitute P0+ρgh1 for Ph1 and amg for Pb in equation (3).
PS=P0+ρgh1+amg
According to Pascal’s law, the pressures PL and PS are equal.
PL=PS
Substitute P0+ρgh for PL and P0+ρgh1+amg for PS in the above equation.
P0+ρgh=P0+ρgh1+amg
⇒ρgh=ρgh1+amg
⇒ρgh−ρgh1=amg
⇒ρg(h−h1)=amg
∴h−h1=aρm
Therefore, the pressure difference between the water levels of the two tubes is aρm.
Hence, the correct option is C.
Note: The students should not forget to include the pressure due to the weight of the block in the pressure of liquid in the smaller tube at depth h1 from the upper edge of the smaller tube. If this value is not included in the pressure of liquid in the smaller tube then the obtained pressure at depth h1 will not be equal to the pressure of liquid in the larger tube at depth h. Hence, the final answer will also be incorrect.
