Question
Question: In the figure shows, pulley and spring are ideal. Find the potential energy stored in the spring (\[...
In the figure shows, pulley and spring are ideal. Find the potential energy stored in the spring (m1>m2)
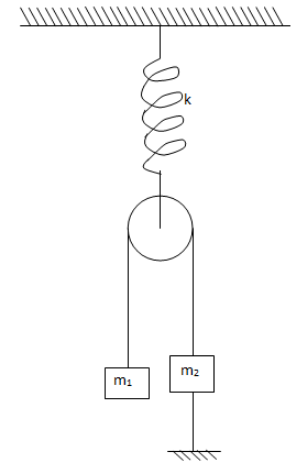
Solution
We are asked to find the potential energy stored in the spring. First, recall the formula to find potential energy stored in a spring. Draw a free body diagram of the problem. Using this diagram, find the value of displacement and use this value to find potential energy of the spring.
Complete step by step answer:
Given a figure where pulley and spring are ideal.The formula to find potential energy stored in a spring is,
P.E=21kx2 (i)
where k is the spring constant and x is the displacement from the mean position.
Let us draw the free body diagram for the problem.
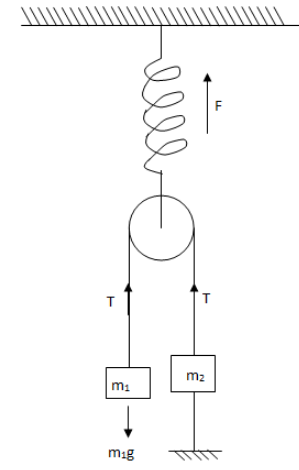
In the figure, F is the restoring force of the spring, T is the tension on the string and g is acceleration due to gravity.
Restoring force is given by the formula,
F=kx (ii)
where k is the spring constant and x is the displacement from the mean position.
From the figure we observe,
T+T=F
Putting the value of F we get,
T+T=kx
⇒2T=kx
⇒T=21kx (iii)
From the figure we get,
T=m1g
Putting the value of T we get,
21kx=m1g
⇒x=k2m1g
Now, putting this value of x in equation (i) we get the potential energy as,
P.E=21k(k2m1g)2
⇒P.E=21k(k24m12g2)
∴P.E=k2m12g2
Therefore the potential energy stored in the spring is k2m12g2.
Note: For such types of problems, before proceeding for calculations, draw a free body diagram. A free body diagram is a diagram showing the forces and their directions acting on a given system. Here we have used the term restoring force, restoring force is the force which brings back an object to its mean position or equilibrium.
