Question

In the figure shown what is the equivalent capacitance between ‘A’ and ‘B’?

A. $3.75\,F$
B. $2\,F$
C. $21\,F$
D. $16\,F$

Answer 1

First redraw the circuit diagram in a simplified manner and label the junctions. Replace series or parallel capacitors with their equivalent capacitors. Continue this process until only one equivalent capacitor is left.

Complete step-by-step answer:
First we redraw the circuit diagram in a simplified manner as shown in figure below.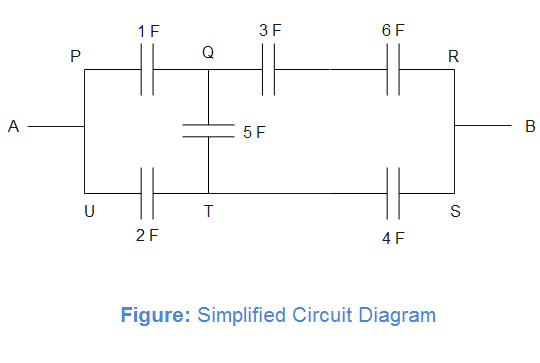
In branch QR two capacitors of 3 F and 6 F are connected in series. We replace these with a capacitor of equivalent capacitance.
Equivalent capacitance of capacitors in series is given as
$\dfrac{1}{{{C}_{QR}}}=\dfrac{1}{3}+\dfrac{1}{6}=\dfrac{2}{6}$
This implies that,
${{C}_{QR}}=2\,F$
Now the circuit becomes as shown below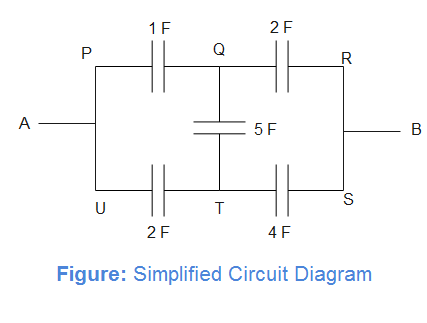
We observe that
$\dfrac{{{C}_{PQ}}}{{{C}_{UT}}}=\dfrac{{{C}_{QR}}}{{{C}_{TS}}}$
This circuit is equivalent to Wheatstone bridge and capacitor in branch QT can be neglected.
Now, capacitors of capacitance 1 F and 2 F in branch PR and capacitors of capacitance 2 F and 4 F in branch US are in series. So equivalent capacitance of branch PR and US is
$\dfrac{1}{{{C}_{PR}}}=\dfrac{1}{1}+\dfrac{1}{2}=\dfrac{3}{2}$
This means ${{C}_{PR}}=\dfrac{2}{3}F$
Similarly, ${{C}_{US}}=\dfrac{4}{3}F$
Now, branches PR and US are connected in parallel. Equivalent capacitance of parallel capacitors is sum of the capacitance of each capacitor. Therefore,
${{C}_{AB}}={{C}_{PR}}+{{C}_{US}}=\dfrac{2}{3}+\dfrac{4}{3}$
On solving this, we get equivalent capacitance between ‘A’ and ‘B’ as
${{C}_{AB}}=2\,F$
Hence, option B is correct.

So, the correct answer is “Option B”.

Note: To solve such problems, first simplify the circuit and then, replace series or parallel capacitors with their equivalent capacitors. Continue this process until only one equivalent capacitor is left.
Similar processes can be carried out for resistors also.