Question

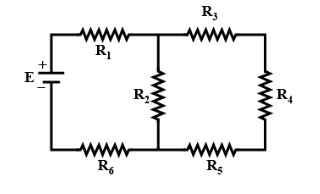
In the figure shown, what is the current (in Ampere) drawn from the battery? You are given:
${R_1} = 15\Omega, {R_2} = 10\Omega, {R_3} = 20\Omega, {R_4} = 5\Omega, {R_5} = 25\Omega, {R_6} = 30\Omega, E = 16V$
A. $\dfrac{7}{18}$
B. $\dfrac{13}{24}$
C. $\dfrac{9}{32}$
D. $\dfrac{20}{3}$

Answer 1

The equivalent resistance in a series combination of n resistors is given by ${R_{eq}} = {R_1} + {R_2} + {R_3} + ..... + {R_n}$
The equivalent resistance in a series combination of n resistors is given by $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ..... + \dfrac{1}{{{R_n}}}$
Total current in circuit is given by $I = \dfrac{E}{{{R_{eq}}}}$ where $E$ is the emf of the battery source and ${R_{eq}}$ of the circuit.

Complete step by step solution:
As from the figure it is clear that ${R_3},{R_4},{R_5}$ are in series and we know that the equivalent resistance in a series combination of n resistors is given by ${R_{eq}} = {R_1} + {R_2} + {R_3} + ..... + {R_n}$
Let $X$ be the equivalent resistance of ${R_3},{R_4},{R_5}$ .
So, $X = 20 + 5 + 25 = 50\Omega$
Now, $X$ and ${R_2}$ is in parallel and we know that the equivalent resistance in a series combination of n resistors is given by $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ..... + \dfrac{1}{{{R_n}}}$
Let $Y$ be the equivalent resistance of $X$ and ${R_2}$
Then, $\dfrac{1}{Y} = \dfrac{1}{X} + \dfrac{1}{{{R_2}}} = \dfrac{1}{{50}} + \dfrac{1}{{10}}$
On simplification, we get $Y = \dfrac{{25}}{3}$
Now, ${R_1},Y,{R_6}$ will be in parallel.
So, the total equivalent resistance of the circuit, ${R_{eq}} = {R_1} + Y + {R_6} = 15 + \dfrac{{25}}{3} + 30$
On simplifying we have ${R_{eq}} = \dfrac{{160}}{3}$
As we know that total current in the circuit is given by $I = \dfrac{E}{{{R_{eq}}}}$ where $E$ is the emf of the battery source and ${R_{eq}}$ of the circuit. This relation is derived from Ohm’s law.
It is given in the question that emf $E = 15V$
So, the current drawn from the battery is $I = \dfrac{{15 \times 3}}{{160}} = \dfrac{9}{{32}}amp$.

$\therefore$ So, the current drawn from the battery is $I = \dfrac{9}{{32}}amp$. Hence, option (C) is the correct answer.

Note:
Ohm’s principal discovery was that the amount of electric current through a metal conductor in a circuit is directly proportional to the voltage impressed across it, for any given temperature. Ohm expressed his discovery in the form of a simple equation, describing how voltage, current, and resistance interrelate:
$E = IR$ where $E$ is the emf of the battery source, $I$ is the current and $R$ is the resistance.