Question

In the figure shown two boats start with different speeds relative to the water simultaneously. The water flow speed is the same for both boats. Mark the correct statements. ${\theta _a}$ and ${\theta _b}$ are angels from the y-axis at which boats are heading at the initial moment.

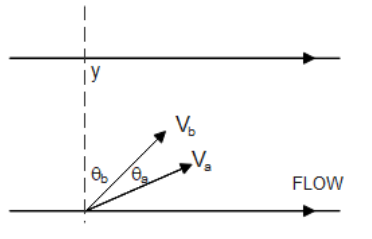
A. If ${V_a} > {V_b}$ then for reaching the other bank simultaneously ${\theta _a} > {\theta _b}$
B. In case the drift of boat A is greater than boat B.
C. If ${V_a} > {V_b}$ and ${\theta _a} > {\theta _b}$ , boat B reaches other banks earlier than boat A
D. If ${V_a} > {V_b}$ and ${\theta _a} > {\theta _b}$, drift A is greater.

Answer 1

To solve such problems we need to have a clear concept of the motion of a boat in a river. It requires us to work with the vector components of velocity. We should be familiar with the concepts of vector addition.

Complete step by step answer:
For reaching the bank simultaneously $y$ displacement should be the same in a time interval.Therefore, the vertical components of velocities of both boats must be equal.
Equating them we get,
${V_b}\cos {\theta _b}t = {V_a}\cos {\theta _a}t$
$\Rightarrow \dfrac{{{V_b}}}{{{V_a}}} = \dfrac{{\cos {\theta _a}}}{{\cos {\theta _b}}}$
For ${V_a} > {V_b}$ implies $\cos {\theta _b} > \cos {\theta _a}$ therefore ${\theta _a} > {\theta _b}$.

And $x$ displacement is the drift produced. For drift, we will consider the horizontal components of velocities.
${V_a}\sin {\theta _a}t$ and ${V_b}\sin {\theta _b}t$
For ${V_a} > {V_b}$ and ${\theta _a} > {\theta _b}$
$\Rightarrow \sin {\theta _a} > \sin {\theta _b}$
Therefore drift A is greater than drift B.

Hence, the correct options are A, B and D.

Additional information: If a motorboat were to head straight across a river (that is if the boat were to point its bow straight towards the other side), it would not reach the shore directly across from its starting point. The river current influences the motion of the boat and carries it downstream. The motorboat may be moving with a velocity of 10m/s directly across the river, yet the resultant velocity of the boat will be greater than 10 m/s and at an angle in the downstream direction. While the speedometer of the boat may read 10 m/s, its speed concerning an observer on the shore will be greater than 10 m/s. And similarly in the case of upstream the velocity will be smaller than the initial velocity of the boat as it sails through the river.

Note: The speed of a boat relative to the water is equal to the speed of the boat in still water. The velocity of a boat relative to the water is equal to the difference in velocity of the boat relative to the ground and velocity of water relative to the ground.