Question
Question: In the figure shown the velocity and pressure of the liquid at the cross section (2) are given by (i...
In the figure shown the velocity and pressure of the liquid at the cross section (2) are given by (if P0 is the atmospheric pressure):
(A) 2hg,P0+2ρhg
(B) hg,P0+2ρhg
(C) 2hg,P0+43ρhg
(D) 2hg,P0+43ρhg
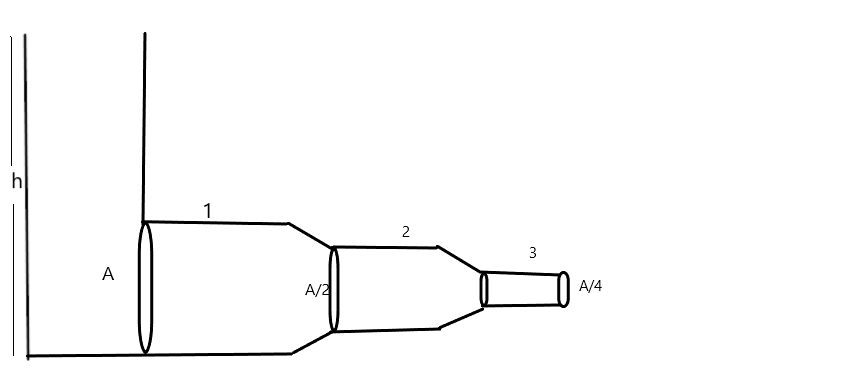
Solution
Viscosity of fluid: It is the property of the fluid by virtue under which an internal force of friction comes into action when the fluid is in motion and which opposes the relative motion between different layers of the fluid.
Streamline flow: It is the specific flow of fluid such that each particle of the liquid passing a given point moves along the same path and has the same velocity as its predecessor.
Equation of continuity: It defines that during a streamline flow of the non-viscous and incompressible fluid through a pipe of varying cross-section, the product of the area of cross-section of the pipe and the normal fluid velocity inside the pipe (av) remains constant throughout the flow.
Bernoulli’s principle: It states that the sum of pressure energy and potential energy per unit volume of an incompressible, non-viscous fluid in a streamlined irrotational flow remains constant along a streamline.
Formula used:
Equation of continuity, a1v1=a2v2, here a1, a2=area of cross-section of the pipe, v1, v2=velocity of the fluid
Bernoulli’s equation, P + 21ρv2+ρgh = constant
HereP= fluid pressure,ρ= density of the fluid, v= velocity of the fluid,
g= Acceleration due to gravity,h= height of the fluid in the pipe
Complete step by step answer:
It is given that P0= atmospheric pressure, A=area of the cross section of region1, A/2=area of the cross section of region2, A/4=area of the cross section of region3
Therefore, we use the above Bernoulli’s equations between the top and point 3,P0+ρgh = P0+21ρv32,
Here at the top of the pipe the velocity (v1) = 0 and the height at point 3, h=0,
We get the value of v3=2gh
By using the equation of continuity between point 1 and point 2, we get,
2Av2=4Av3
⇒v2=2v3
Substituting the value of v3 in the equation we get,
v2=22gh
⇒2gh
We use the above Bernoulli’s equations between the top and point 2,
P0+ρgh = P2+21ρv22,
Here at the top of the pipe the velocity (v1) = 0 and the height at point2, h=0, we get the value of P2,
P2=P0+ρgh - 21ρv22,
Now we will substitute the value of v2 in the equation
⇒P2=P0+ρgh - 21ρ(2gh)
On multiplying the terms we get,
⇒P2=P0+ρgh−4ρgh
Taking LCM on the second and third term we get,
⇒P2=P0+43ρgh
Hence velocity 2gh and pressure of the liquid P2=P0+43ρgh
∴ The correct option is (C).
Note:
Bernoulli’s equation is derived from the assumption that there is no loss of energy due to friction among fluid particles.
Some of the kinetic energy converted into heat energy due to the work done against the internal energy or friction or the viscous forces.
The angular momentum of the fluid is not taken into consideration in Bernoulli’s equation.
