Question

In the figure shown, the mass of the disc as well as that of the trolley is M. The spring is ideal and has stiffness k. The trolley can move horizontally on the floor without friction, and the disc can roll on the trolley surface without slipping. The spring is compressed and the system released so that oscillations begin. At the instant of release, magnitude of:

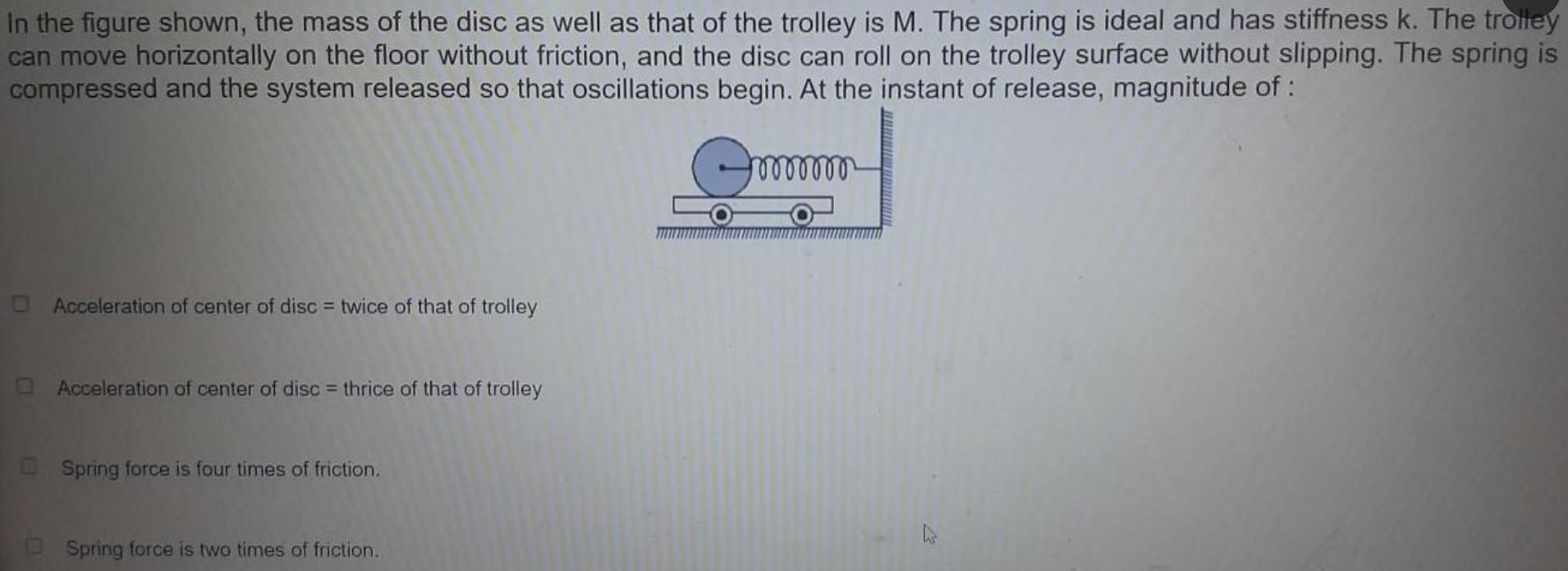
• A. Acceleration of center of disc = twice of that of trolley
• B. Acceleration of center of disc = thrice of that of trolley
• C. Spring force is four times of friction.
• D. Spring force is two times of friction.

Answer 1

Answer: (B), (C)

Acceleration of center of disc = thrice of that of trolley Spring force is four times of friction.

Answer 2

Let • a_d = acceleration of disc’s center (relative to ground) • a_t = acceleration of trolley • f = friction force between disc and trolley • kx = spring force

For a disc of mass M and moment of inertia I = ½MR² with no‐slip on a moving platform, the rolling constraint gives:   (a_d – a_t) = Rα and the rotation equation (about its center) is:   fR = Iα = ½MR²·(a_d–a_t)/R   ⟹ f = ½M (a_d – a_t).

Now, taking directions to the right as positive and noting that when the spring (attached to the disc) is released its force kx acts to the right, we write the equations:

1. For the disc (translation):   M a_d = kx – f                (1)

2. For the trolley (it only feels the friction from the disc):   M a_t = f                    (2)

Substitute f from above into (2):   a_t = ½ (a_d – a_t)   ⟹ 2a_t = a_d – a_t   ⟹ a_d = 3a_t.

Then, from (2):   f = M a_t.

Substitute a_d = 3a_t and f = M a_t into (1):   M (3a_t) = kx – M a_t   ⟹ kx = 3M a_t + M a_t = 4M a_t Since f = M a_t, we have   kx = 4f.

Thus:

• The acceleration of the disc’s center is 3 times that of the trolley.
• The spring force is 4 times the friction force.