Question

In the figure shown, the mass of the disc as well as that of the trolley is M. The spring is ideal and has stiffness k. The trolley can move horizontally on the floor without friction, and the disc can roll on the trolley surface without slipping. The spring is compressed and the system released so that oscillations begin. At the instant of release, magnitude of:

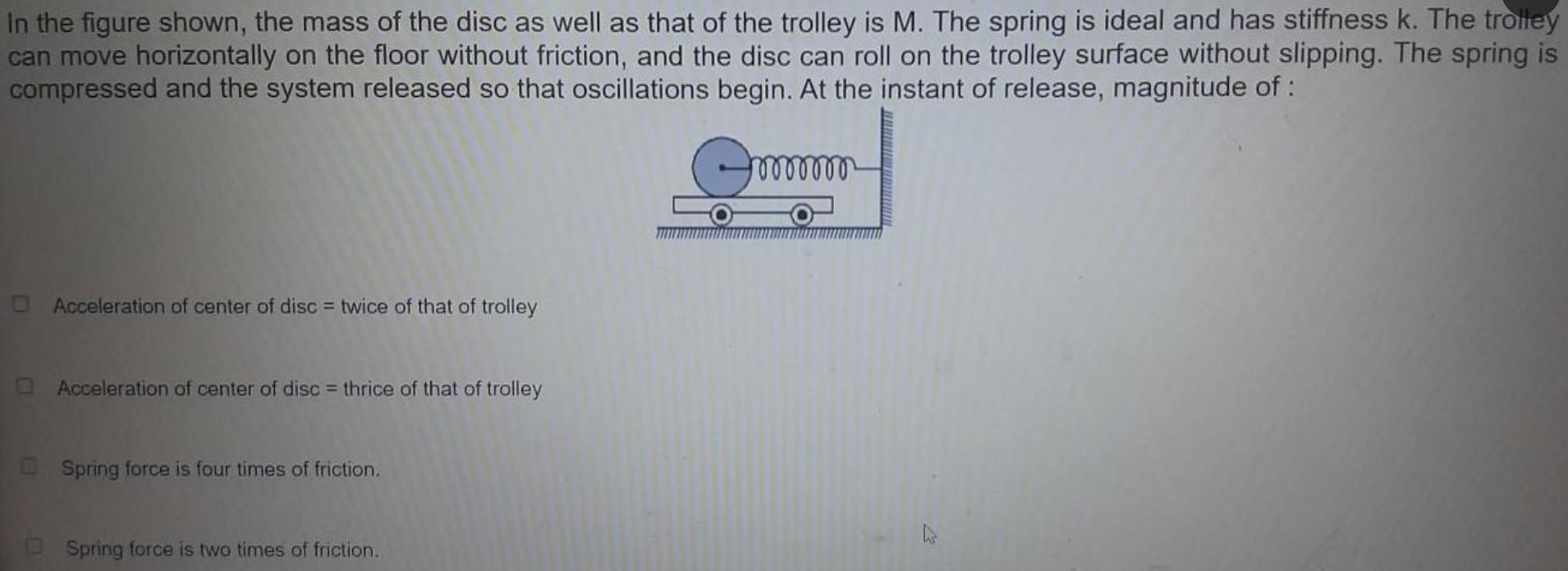
• A. Acceleration of center of disc = twice of that of trolley
• B. Acceleration of center of disc = thrice of that of trolley
• C. Spring force is four times of friction.
• D. Spring force is two times of friction.

Answer 1

Answer: (B), (C)

Options (2) and (3)

Answer 2

Let the trolley have acceleration $a_t$ and the disc’s center have acceleration $a_d$. For rolling without slipping on the trolley, the relative acceleration of the disc is

$$a_d - a_t = R\,\alpha.$$

The torque on the disc due to friction $f$ is

$$fR = I\alpha,$$

where $I=\tfrac{1}{2}MR^2$. Thus,

$$\alpha = \frac{2f}{MR}.$$

So,

$$a_d - a_t = R\left(\frac{2f}{MR}\right) = \frac{2f}{M}.$$

Write the equations of motion:

• For the disc (mass $M$): The net force is the spring force $F=kx$ acting to the right minus friction $f$ acting to the left:

$$M a_d = F - f.$$

• For the trolley (mass $M$): The only horizontal force is the friction $f$ (by Newton’s third law, equal and opposite to that on the disc) so that

$$M a_t = f.$$

Substitute $f = Ma_t$ into the rolling condition:

$$a_d - a_t = \frac{2(Ma_t)}{M} = 2a_t \quad\Longrightarrow\quad a_d = 3a_t.$$

Substitute $a_d = 3a_t$ into the disc’s equation:

$$M(3a_t) = F - Ma_t \quad\Longrightarrow\quad F = 4Ma_t.$$

Since $f = Ma_t$, we have

$$F = 4f.$$

Thus, the correct relationships are:

• The acceleration of the disc’s center is three times that of the trolley.
• The spring force is four times the friction force.