Question
Question: In the figure shown, the capacity of the condenser C is \(2\mu F\) . The current in resistance is \(...
In the figure shown, the capacity of the condenser C is 2μF . The current in resistance is 2Ω .
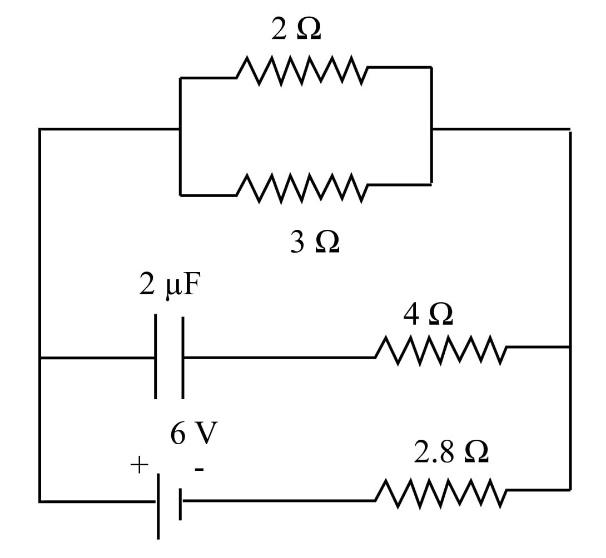
A.9A B.0.9A C.91A D.0.91A
Solution
This question is from the chapter current electricity. We have been given a circuit in which we have to find the current in one of the branches. Here we have to apply the concepts of steady state in a circuit, combination of resistors and the Ohm's law. With these we have to calculate the current passing through the resistor 2Ω.
Complete step by step answer:
In this circuit if we consider the case of the steady state, then the branch with the capacitor will act like an open circuit. Since it will act like an open circuit, no current will pass through the branch in which the capacitor is connected. Therefore, if we neglect that branch, we have three resistors out of which two are in parallel and one is in series with them, to calculate the equivalent resistance we will use the formula as follows:
Equivalent resistance of the two resistors connected in parallel combination:
Req1=R11+R21 ⟹Req1=21+31 ⟹Req1=63+62 ⟹Req1=65 ⟹Req=56Ω ⟹Req=1.2Ω
We have found the equivalent resistance of the two resistors in parallel and they are in series with the other resistor so we will use the formula of the series combination:
Req=R1+R2 ⟹Req=1.2+2.8 ⟹Req=4Ω
Therefore, now we have the equivalent resistance of the whole circuit and by using the Ohm's law we can calculate the current. The mathematical representation of the Ohm's law is:
V=IR
Putting the values of the potential of the battery and the equivalent resistance we get:
V=IR ⟹6=I×4 ⟹I=46A ⟹I=1.5A
Therefore, the value of the current in the whole circuit is 1.5 A. We have to find the value of the current in the 2Ω resistor. For this we will again use the current divider rule for the branches which are in parallel combination:
I2Ω=Icircuit×(ReqofbranchesRoppositebranch) ⟹I2Ω=1.5×(53) ⟹I2Ω=0.9A
Therefore, the current in the resistor of 2Ω is 0.9A. And the correct option is option B.
Note:
In questions like this we have to visualize the circuit for ourselves and we have to apply the appropriate formulas. For such questions we have to consider the condition of steady state and then try to solve the question. Also, we have used the current divider rule for calculating the current in the parallel combination to save our time. If we use the traditional Ohm's law it would have taken a lot more time than this method.
