Question
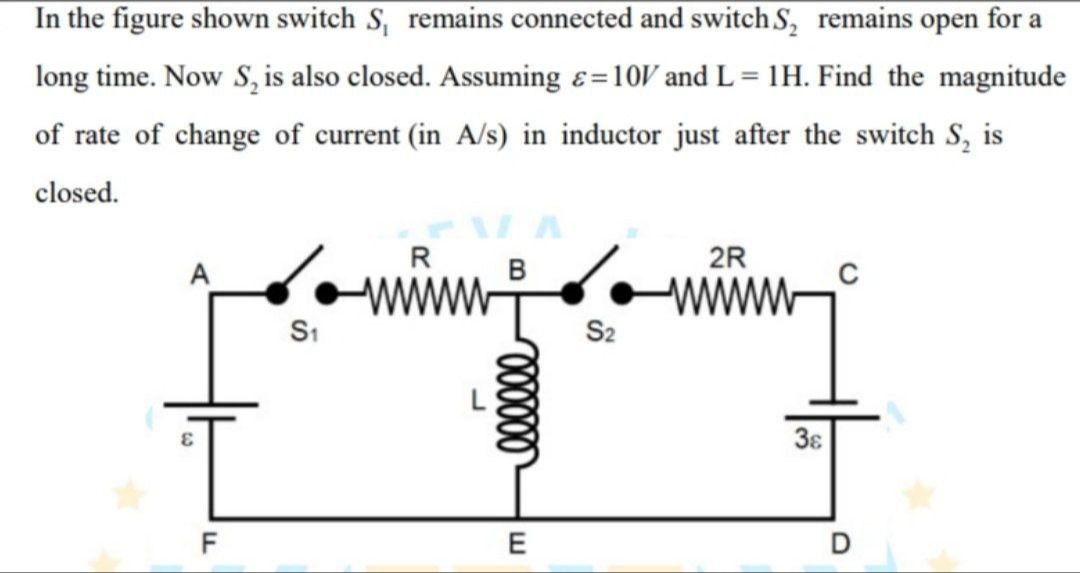
Question: In the figure shown switch \(S_1\) remains connected and switch \(S_2\) remains open for a long time...
In the figure shown switch S1 remains connected and switch S2 remains open for a long time. Now S2 is also closed. Assuming ε=10V and L=1H. Find the magnitude of rate of change of current (in A/s) in inductor just after the switch S2 is closed.
10 A/s
Solution
Solution:
-
Before closing S₂:
– With S₁ closed and S₂ open for a long time, the inductor is in DC steady state so it behaves like a short.
– The inductor current becomes
IL(0−)=Rε=R10. -
Immediately after S₂ is closed (t = 0⁺):
– Now node B is connected to two branches:
- Left branch: 10 V source with resistor R, current = (10−VB)/R.
- Right branch: 30 V source (3ε) with resistor 2R, current = (30−VB)/(2R).
– Applying KCL at node B (with the inductor current IL=10/R unchanged due to current continuity):
R10−VB+2R30−VB=R10.– Multiply through by 2R:
2(10−VB)+(30−VB)=20.This simplifies to:
20−2VB+30−VB=20⇒50−3VB=20.Thus,
3VB=30⇒VB=10V. -
Rate of Change of the Inductor Current:
– The voltage across the inductor is VL=VB=10V.
– Using the inductor relation
VL=LdtdI,with L=1H, we have
dtdI=110=10A/s.
Core Explanation (Minimal):
- Before S₂ closes, IL=10/R.
- At t = 0⁺, applying KCL at node B gives VB=10V.
- Thus, by VL=LdtdI → dtdI=10A/s.
