Question

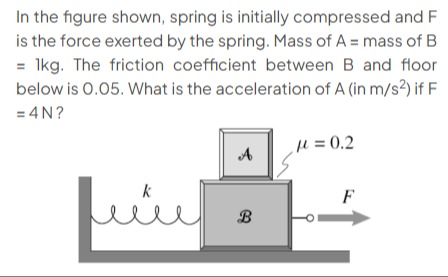
In the figure shown, spring is initially compressed and F is the force exerted by the spring. Mass of A = mass of B = 1kg. The friction coefficient between B and floor below is 0.05. What is the acceleration of A (in m/s²) if F = 4 N?

Answer 1

1.5

Answer 2

To determine the acceleration of block A, we need to analyze the forces acting on both blocks and consider the friction between the surfaces.

Given data:

• Mass of A, $m_A = 1 \text{ kg}$
• Mass of B, $m_B = 1 \text{ kg}$
• Friction coefficient between B and floor, $\mu_{B,floor} = 0.05$
• Friction coefficient between A and B, $\mu_{A,B} = 0.2$
• Force exerted by the spring, $F = 4 \text{ N}$ (acting to the right on block B)
• Assume acceleration due to gravity, $g = 10 \text{ m/s}^2$.

Step 1: Analyze forces on block A

Block A is on top of block B.

• Vertical forces:
  The normal force exerted by B on A, $N_A$, balances the weight of A.
  $N_A = m_A g = 1 \text{ kg} \times 10 \text{ m/s}^2 = 10 \text{ N}$
• Horizontal forces:
  The only horizontal force on A is the static friction force $f_{BA}$ exerted by B on A. This force tries to make A move along with B.
  The maximum static friction force between A and B is:
  $f_{s,max,AB} = \mu_{A,B} N_A = 0.2 \times 10 \text{ N} = 2 \text{ N}$
  If A moves with acceleration $a_A$, then $f_{BA} = m_A a_A$. For A not to slip on B, $f_{BA} \le f_{s,max,AB}$.
  Therefore, $m_A a_A \le 2 \text{ N} \implies 1 \text{ kg} \times a_A \le 2 \text{ N} \implies a_A \le 2 \text{ m/s}^2$.
  This means if the acceleration of block B (and A, assuming they move together) is less than or equal to $2 \text{ m/s}^2$, A will move with B. If it's greater, A will slip, and its acceleration will be $2 \text{ m/s}^2$.

Step 2: Analyze forces on block B

• Vertical forces:
  The normal force exerted by the floor on B, $N_B$, balances the weight of B and the normal force exerted by A on B ($N_{AB}$). By Newton's third law, $N_{AB} = N_A = 10 \text{ N}$.
  $N_B = m_B g + N_{AB} = (1 \text{ kg} \times 10 \text{ m/s}^2) + 10 \text{ N} = 10 \text{ N} + 10 \text{ N} = 20 \text{ N}$

• Horizontal forces:

  1. Force from spring, $F = 4 \text{ N}$ (to the right).
  2. Friction force from A on B, $f_{AB}$ (to the left, opposite to $f_{BA}$).
  3. Friction force from floor on B, $f_{B,floor}$ (to the left, opposing motion).

  The maximum static friction force between B and the floor is:
  $f_{s,max,B,floor} = \mu_{B,floor} N_B = 0.05 \times 20 \text{ N} = 1 \text{ N}$

Step 3: Determine if the blocks move together and calculate acceleration

Let's assume A and B move together with a common acceleration $a$. We can treat (A+B) as a single system with total mass $M = m_A + m_B = 1 \text{ kg} + 1 \text{ kg} = 2 \text{ kg}$.

• Check if the system moves:
  The applied force on the system is $F = 4 \text{ N}$. The maximum static friction opposing motion from the floor is $f_{s,max,B,floor} = 1 \text{ N}$.
  Since $F (4 \text{ N}) > f_{s,max,B,floor} (1 \text{ N})$, the system will move.
  Therefore, the friction force from the floor will be kinetic friction: $f_{B,floor} = f_{k,B,floor} = 1 \text{ N}$.

• Apply Newton's second law to the combined system (A+B):
  Net force = (Total mass) $\times$ (Common acceleration)
  $F - f_{B,floor} = (m_A + m_B) a$
  $4 \text{ N} - 1 \text{ N} = (1 \text{ kg} + 1 \text{ kg}) a$
  $3 \text{ N} = 2 \text{ kg} \times a$
  $a = \frac{3}{2} \text{ m/s}^2 = 1.5 \text{ m/s}^2$

• Check for slipping between A and B:
  For block A to move with this common acceleration $a = 1.5 \text{ m/s}^2$, the static friction force required from B on A is:
  $f_{BA} = m_A a = 1 \text{ kg} \times 1.5 \text{ m/s}^2 = 1.5 \text{ N}$
  We compare this required friction force with the maximum static friction available between A and B, $f_{s,max,AB} = 2 \text{ N}$.
  Since $1.5 \text{ N} < 2 \text{ N}$, the static friction is sufficient to prevent A from slipping on B.
  Therefore, block A moves together with block B, and its acceleration is $1.5 \text{ m/s}^2$.

The final answer is $\boxed{1.5}$

Explanation of the solution:

1. Calculate normal force on A ($N_A = m_A g$) and maximum static friction between A and B ($f_{s,max,AB} = \mu_{A,B} N_A$). Determine the maximum acceleration A can have without slipping on B ($a_{max,A} = f_{s,max,AB}/m_A$).
2. Calculate normal force on B ($N_B = m_B g + N_A$) and maximum static friction between B and floor ($f_{s,max,B,floor} = \mu_{B,floor} N_B$).
3. Treat A and B as a single system. Check if the applied force ($F$) is greater than the maximum static friction from the floor. If yes, the system moves, and kinetic friction applies.
4. Apply Newton's second law to the combined system to find their common acceleration ($a = (F - f_{k,B,floor}) / (m_A + m_B)$).
5. Compare this common acceleration with $a_{max,A}$. If $a \le a_{max,A}$, then A does not slip, and its acceleration is $a$.

Answer:
The acceleration of A is $1.5 \text{ m/s}^2$.